VIVOS VOCO: Ю.И. Головин, А.И. Тюрин, "Микро- и наноконтактное взаимодействие твердых тел"

Микро- и наноконтактное
взаимодействие твердых тел

Ю.И. Головин, А.И. Тюрин

Юрий Иванович Головин, д.ф.-м.н., профессор,
заслуженный деятель науки Российской Федерации,
зав. каф. теоретической и экспериментальной физики
Тамбовского государственного университета.

Александр Иванович Тюрин, к.ф.-м.н.,
доцент, докторант той же кафедры.

Человек знакомится с контактным взаимодействием различных тел и испытывает его на самом себе буквально с первых шагов по Земле, отталкиваясь от нее за счет сил трения, набивая шишки об острые предметы, пробуя “на зуб” прочность любимых игрушек, вскрикивая от боли, когда жалит пчела, и т.п. Простейшие технологии обработки материалов и изготовления орудий труда путем обкалывания камней и обтесывания деревяшек, дробления сырья (например, зерна) включали как основной элемент ударное контактное взаимодействие. На протяжении тысячелетий его использовали и в вооруженных столкновениях с применением холодного оружия (стрелы, копья, тарана). В эпоху машин, механизмов и даже компьютеров и роботов роль процессов, происходящих при контактировании различных элементов между собой и с окружающими предметами, нисколько не уменьшается. Более того, она даже возрастает, а физические процессы в контакте интенсифицируются и усложняются в связи с ростом нагрузок, скоростей, числа активно действующих факторов и др. Однако что мы знаем о природе кратковременных контактов реальных тел в настоящее время?

От объема - к поверхности, от поверхности - к точке

Механическое, механохимическое, гальваническое взаимодействия твердых тел в процессе их контактирования происходят первоначально в небольшом числе точек, воспринимающих всю нагрузку (рис.1,а). При этом в областях с субмикронными характерными размерами развиваются напряжения, близкие к теоретическому пределу прочности (порядка нескольких процентов от модуля Юнга), и относительные деформации e в десятки процентов. (Напомним, что интенсивность деформации определяется безразмерной величиной e = DL/L, где DL - изменение исходного размера L.) Причем подобные напряжения возникают даже в таких хрупких и не деформируемых пластически (в обычных условиях) материалах, как карбиды или бориды тугоплавких металлов.

Рис.1. Примеры ситуаций, в которых реализуется наноконтактное взаимодействие (v - линейная скорость, w - угловая скорость; тонкая штриховка обозначает области высокой локальной деформации):
а - сухое трение, абразивный износ при латеральном перемещении одной микрошероховатой поверхности по другой;
б - эрозионный износ поверхности мелкими частичками, бомбардирующими ее под разными углами;
в - локальная приповерхностная усталость, фреттинг под действием знакопеременной локальной нагрузки;
г - тонкий помол, механохимический синтез продуктов в шаровой мельнице, осуществляемый за счет кратковременного ударного контактирования твердых шаров;
д - исследование и модификация поверхности атомно-острыми иглами в туннельных и атомно-силовых микроскопах;
е - наноконтакт в области соприкосновения двух фуллереновых нанотрубок.

По мере удаления от точки контакта напряжения и деформации быстро падают и не представляют уже никакой опасности для материала. Благодаря крайней малости локально деформированной области (R<1 мкм) скорость относительной деформации, определяющая атомные механизмы пластического течения, e· = de/dt = = dR/R·dt = v/R (даже при невысоких скоростях абсолютного перемещения v<1 м/с) достигает значений 10⁶ с^–1, характерных для деформации детонирующим взрывчатым веществом (рис.2). Таковы условия при сухом трении одного тела по поверхности другого, механическом шлифовании, абразивном износе (например, при движении ленты вдоль магнитных головок в магнитофоне), при накоплении повреждений в результате соударения пылинок с поверхностью движущихся транспортных средств (в том числе и космических), при тонком помоле в различных мельницах и в активаторах механохимических реакций, в контактных модах зондовой атомно-силовой микроскопии и при модификации поверхности, в вершине быстро растущей квазихрупкой трещины и во многих иных ситуациях (рис.1). Атомарные процессы, которые происходят при этом в тонких приповерхностных слоях, определяют служебные свойства изделия, его долговечность, износостойкость, коэффициент трения, химическую и каталитическую активность поверхности, ее способность эмитировать электроны и другие частицы, а также многое другое. До последнего времени эти процессы изучались главным образом феноменологически на макроуровне путем усреднения характеристик по всей кажущейся поверхности контакта. Поэтому большинство подобных проблем находилось в ведении инженеров-механиков, технологов, электриков.

Рис.2. Связь скорости относительной деформации e с характерными размерами объектов для некоторых процессов (ВВ - взрывчатое вещество).

С начала 90-х годов прошлого века к изучению контактных взаимодействий стали привлекать современные физические методы, обладающие нанометровым разрешением (такие как сканирующая туннельная и атомно-силовая микроскопия, наноиндентирование) [1, 2]. Впервые со времен Гильома Амонтона - гениального французского физика-самоучки, создателя первого учения о трении (1699) - появилась возможность перейти от усредненных по поверхности характеристик трения, износа, электрического сопротивления и т.п. к локальным их значениям и заполнить брешь между макроскопическим и атомарным описанием этих сложных процессов.

Потребности нанотехнологии, наноматериаловедения, миниатюризации элементной базы микроэлектроники и оптотроники, создание интегрированных микроэлектромеханических систем, интеллектуальных микророботов заставили в последние годы резко активизировать работы по изучению явлений на уровне отдельных элементарных событий в одном микро- (или нано-) контакте. В частности, технологии исследования и модификации приповерхностных слоев, использующие атомно-острые иголки, локализуют воздействие в объемах нанометрового масштаба и должны учитывать большую разницу в механических и других свойствах материала при переходе от макро- к наномасштабам объекта.

Мы не будем обсуждать здесь хорошо развитые “неразрушающие” методы сканирующей зондовой микроскопии (хотя то, в какой мере они не повреждают поверхность, всегда остается под вопросом), а рассмотрим методы, основанные на прецизионном локальном силовом воздействии на исследуемую поверхность (рис.3).

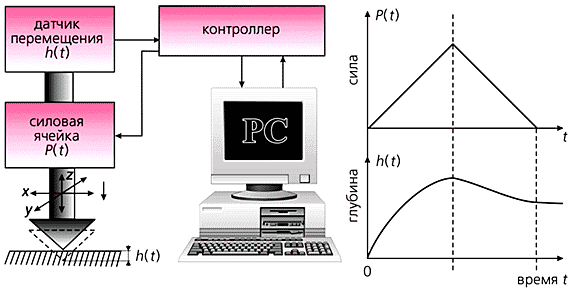
Рис.3. Принципиальная схема нанотестирования поверхности (слева)
и временнЫе зависимости усилия Р и глубины погружения h
при внедрении индентора по нормали к поверхности (справа).

Невиданные возможности

Благодаря удобству, гибкости, отсутствию жестких требований к образцу и окружающей среде методы наноиндентирования приобрели большую популярность в последние несколько лет [3-8]. Они позволяют приблизиться к условиям, возникающим в реальных микро- и наноконтактах, и смоделировать при хорошо контролируемых условиях элементарные процессы в областях, сильно деформированных высокой локальной нагрузкой.

В соответствии с направлением движения зондирующего поверхность инструмента (чаще всего это хорошо аттестованная трехгранная алмазная пирамидка Берковича) по отношению к плоскости образца их подразделяют на наноиндентирование (индентор движется по нормали к поверхности) и наносклерометрию (индентор движется по касательной к поверхности). Сущность этих методов состоит в программируемом приложении малых или ультрамалых усилий к индентору и непрерывной регистрации зависимости силы сопротивления Р от смещения (глубины погружения h или тангенциального перемещения x). Типичные записи диаграмм для обоих случаев показаны на рис.4.

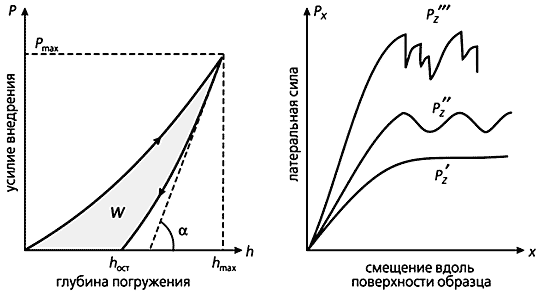
Рис.4. Типичные диаграммы сила-перемещение при наноиндентировании (слева) и наноскрабировании (справа).

h_max - максимальная глубина погружения индентора,
h_ост - глубина отпечатка, оставшегося после снятия нагрузки.
W - поглощенная энергия. P’_z , P’_{z ’}, P’_{z ’’}, - низкие, умеренные и высокие значения силы прижима индентора к поверхности соответственно.

Коммерческие нанотестеры таких известных фирм, как MTS, “Hysitron”, “Micro Photonics”, “CSM Instruments” и др., имеют разрешение в канале измерения силы около 1 нН, а по перемещению - значительно лучше, чем 1 нм (т.е. близкое к атомному). Многие принципиальные и конструктивные решения в нанотестерах близки к используемым в зондовой сканирующей микроскопии, и ряд производителей объединяют оба типа испытания в одном комбинированном приборе. Это позволяет не только визуализировать микротопографию поверхности, но и исследовать более десятка механических характеристик материала в приповерхностных слоях, покрытиях, пленках толщиной от единиц нанометров до нескольких микрометров, т.е. перейти от двумерного к трехмерному анализу приповерхностных слоев материала. В частности, обработка P-h диаграмм, полученных при наноиндентировании, дает возможность определять сопротивление упругопластическому локальному деформированию в наноконтакте и осуществлять экспериментальную проверку имеющихся теорий микро- и наноконтактного взаимодействия. Отношение приложенной нагрузки Р к площади контакта S характеризует нанотвердость H=P/S при упругопластическом контакте, а площадь петли полного цикла нагружение-разгрузка в координатах P-h (рис.4, слева) - поглощенную в контактном взаимодействии энергию W. По данным непрерывного наноиндентирования можно восстанавливать кривые активного деформирования s = f(e) и ползучести e = f(t) материалов, не поддающихся пластическому деформированию в макроопытах из-за опережающего квазихрупкого разрушения (керамик, минеральных и металлических стекол, карбидов, нитридов, боридов тугоплавких металлов и т.д.). Этим методом также определяют характеристики подвижности дислокаций в кристаллических материалах и коэффициент вязкости разрушения К_1с (по размерам трещин вокруг отпечатка и величине силы вдавливания). Путем многократного нагружения одной и той же области или нанесения наноцарапин моделируют процессы износа и усталости в приповерхностных слоях, изучают фазовые переходы, индуцированные высоким гидростатическим давлением под индентором, исследуют зависящие от времени характеристики материала и коэффициенты скоростной чувствительности механических свойств как на стадии погружения, так и на стадии вязкоупругого восстановления отпечатка после разгрузки. Методом наноиндентирования можно также оценивать пористость материала, величину и распределение внутренних напряжений, толщину, степень адгезии и механические свойства тонких слоев и покрытий, исследовать структуру многофазных материалов, определять модули упругости, скорость звука и анизотропию механических свойств, а также многое другое.

Упомянем несколько характерных примеров конкретного использования нанотестеров для исследования свойств материалов в тонких приповерхностных слоях. Во многих работах исследовали и анализировали причины масштабного эффекта (indentation size effect) - роста твердости при низких и сверхнизких усилиях внедрения (порядка микроньютона), которые приводят к образованию отпечатков нанометровой глубины. При нагрузках ниже некоторых критических (зависящих от природы материала, температуры, формы индентора и т.д.) практически все материалы начинают демонстрировать в контакте упругое поведение. Типичные значения критической неразрушающей глубины составляют обычно несколько десятков нанометров [4]. По начальному наклону кривой усилие-глубина на стадии разгрузки (угол a на рис.4, слева) можно определить пористость и модуль Юнга в области с размерами меньше микрометра. Большое число работ посвящено исследованиям методами наноиндентометрии свойств тонких пленок, покрытий, эпитаксиальных слоев на поверхности твердых тел. Кроме собственно нанотвердости, обычно определяют степень адгезии, модуль Юнга, плотность, однородность. Рекордными к настоящему времени, по-видимому, являются измерения, проведенные на пленках толщиной в единицы нанометров.

Методами локальных измерений электросопротивления и спектров рамановского рассеяния были обнаружены и исследуются in situ фазовые переходы в GaAs, Ge, Si, SiC, кварце, алмазе и др., индуцированные высоким давлением в зоне деформации под индентором. Так, например, в кремнии наблюдается до пяти фаз высокого давления и аморфизация исходной монокристаллической структуры.

Влияние скорости деформирования на механические свойства различных материалов при индентировании изучается в весьма широком диапазоне относительных скоростей деформаций (10^–4-10⁺¹ с^–1). Определены коэффициенты скоростной чувствительности твердости, предела текучести, степени упрочнения и т.д. Однако скорости в этих исследованиях пока ограничены сверху значениями, недостаточными для моделирования микро- и наноконтактного взаимодействия во многих важных случаях. Да и физические процессы, происходящие в реальных наноконтактах и даже в хорошо контролируемых условиях наноиндентирования в зоне локальной деформации, во многом остаются малоизученными. В частности, неясно, до какого масштаба объекта сохраняются механические свойства материала (т.е. до каких пор можно опираться на данные, полученные в макроопытах). Какова структура материала под индентором и куда девается материал из-под него в случае отсутствия “навалов” вокруг отпечатка? В чем роль возможных фазовых переходов, индуцируемых высокими давлениями и сдвиговыми напряжениями, в формировании локальных механических свойств? Большинство из этих вопросов сводятся к одному, принципиально важному: каковы атомные механизмы пластической деформации в локально деформированной зоне, зависят ли они от ее размеров и скорости деформации?

Предел текучести и нанотвердость - ближайшие родственники?

С первых шагов исследования твердости различных материалов предполагалось, что ее величина Н должна быть определенным образом связана с пределом текучести s_у при одноосном растяжении/сжатии макрообразцов. Так, было установлено, что для большинства металлов и сплавов Н=Аs_у, где А~”3. Поскольку величина s_у в металлах определяется главным образом процессами размножения специфических квазиодномерных дефектов кристаллической структуры - дислокаций, твердость также стали связывать с поведением дислокационных ансамблей. Впоследствии эти представления были молчаливо распространены (заметим, без достаточных на то оснований) и на другие материалы и ситуации. Учитывая широкий спектр современных материалов, исследуемых в настоящее время методами наноиндентирования, случаи, когда А = const ~ 3, следует считать скорее исключением, чем правилом. Например, в ионных кристаллах зачастую полностью отсутствует однозначная связь между Н и s_у. Различные способы их упрочнения (предварительное деформирование, понижение температуры испытания, легирование, облучение), дающие одинаковый прирост sу, оказывают совершенно разное влияние на Н, и одним и тем же значениям Н могут отвечать сильно отличающиеся величины s_у, а при неизменном значении s_у могут наблюдаться изменения Н более чем на порядок величины. При этом отношение H/s_у может достигать >10². Все это наглядно демонстрирует отсутствие простой и однозначной связи между Н и s_у в общем случае и указывает на различную природу этих характеристик материала.

В более жестких кристаллах (Ge, Si, Al₂O₃), карбидах, боридах, нитридах, многокомпонентных керамиках дислокации если и появляются вокруг отпечатка, то их так мало, что они заведомо не могут существенно повлиять на твердость. В работе [8] приводятся оценки возможной роли дислокаций при поглощении энергии W (а следовательно, и при формировании значения твердости Н, поскольку Н~W) для локального нагружения монокристаллического Ge и циркониевой керамики. По оценке сверху, даже при повышенных температурах (до 400°С для Ge и 800°С для ZrO₂) вклад дислокаций не превышает единиц процентов.

Простые оценки устойчивости дислокационной петли в поле внешних и собственных внутренних напряжений (последние возникают вследствие большого линейного натяжения, которое делает дислокационную линию похожей на сильно растянутое резиновое колечко, закрепленное в кристалле другими дефектами в нескольких точках) показывают, что зарождение и существование в кристалле петель с размерами менее нескольких нанометров энергетически невыгодно. Ситуация здесь совершенно аналогична той, что возникает при фазовых переходах первого рода, нуждающихся в генерации зародышей новой фазы закритических размеров. Так, для закипания жидкости необходимо образование паровых пузырьков с радиусом больше критического, а для инициирования дислокационной пластичности - генерирование петель закритических размеров. Если область локальной деформации имеет размеры меньше критических для дислокаций в данном кристалле, то последние не могут образоваться в принципе.

Следует отметить, что картина локальной деформации может значительно осложниться за счет развития различного рода неустойчивостей и самоорганизации отдельных событий. При погружении индентора нормально к поверхности природа деформации может быть обусловлена взрывообразным размножением дислокаций, их деформационным старением и закреплением диффундирующими точечными дефектами, фазовыми переходами, индуцированными высокими давлениями, зарождением микротрещин и т.д. При боковом движении индентора явления неустойчивости могут приобрести еще более разнообразный характер. Ясно, что на фундаментальном уровне взаимодействия атомарно гладких поверхностей должен проявляться эффект неравномерности движения с периодичностью кристаллической решетки в этом направлении (что реально и наблюдается в латеральной контактной моде атомно-силовой микроскопии). При взаимодействии шероховатых поверхностей макроскопически плавное скольжение, как правило, в действительности состоит из чередующихся отдельных актов прилипания - скачкообразного отрыва (stick-slip effect). (Вспомните простейший опыт - генерацию звука при движении пальца по сухому стеклу.) В результате возникает необходимость включить в рассмотрение и адгезионные явления, и процессы образования разрывающихся “мостиков” в микроконтактах.

Наноконтакты “on line”

Известны попытки исследовать динамику внедрения индентора, скачки и нестабильность локальной деформации in situ посредством стандартных нанотестеров с непрерывной записью глубины отпечатка во времени. Однако недостаточное временнОе разрешение (~0.1 с) ограничивало сверху доступный для исследования диапазон e· величиной ~10¹ с^–1 и не позволяло регистрировать динамический отклик материала на самой интересной, начальной стадии погружения.

В лаборатории наноиндентирования Тамбовского государственного университета разработан ряд оригинальных методик и динамических наноиндентометров, обладающих не только высоким пространственным, но и временнЫм разрешением (в некоторых моделях - до 1 мкс), что дает возможность исследовать скоростные зависимости свойств материалов в субмикрообластях при e· до 10⁴-10⁵ с^–1 [9-14].

Упоминавшаяся выше неправомерность рассмотрения a priori процесса индентирования как автомодельного диктует необходимость специального изучения начальных стадий погружения с адекватным пространственно-временны?м разрешением. Как известно, наиболее полно и просто динамические свойства системы могут быть исследованы путем анализа ее отклика на скачкообразное возмущение. В одном из разработанных методов реализован этот подход: постоянная испытательная нагрузка прикладывается к индентору скачкообразно, и кинетика его погружения в материал регистрируется непрерывно (рис.5).

Рис.5. Динамический отклик приповерхностных слоев материала на кратковременно приложенное постоянное локальное усилие Р. h(t) - глубина погружения, t - длительность прямоугольного импульса нагрузки.

Разработанные нанотестеры позволяют также варьировать в широких пределах длительность воздействия треугольных импульсов нагрузки (от 1 мс до 1000 с), осуществлять нагружение с постоянной скоростью относительной деформации ·e, проводить микроконтактные усталостные испытания (путем многократно повторяющегося нагружения одной и той же области образца), определять величину энергии, поглощенной при локальном деформировании, и т.д. Сочетание перечисленных выше методик дает возможность исследовать в совокупности комплекс динамических свойств, недоступный квазистатическим методам.

При испытаниях прямоугольным импульсом силы на кинетических кривых погружения индентора в полулогарифмических координатах lg e· = f(t) (рис.6) отчетливо различимы несколько участков с разным наклоном, которые можно отождествить с отдельными стадиями в процессе формирования отпечатка. Близкий к линейному закон падения во времени lg e· на каждом из выявленных участков отражает экспоненциальный характер релаксации. Различие в показателе экспоненты на разных стадиях достигает четырех порядков величины, а в предэкспоненциальном множителе - более пяти порядков величины. Ясно, что в условиях практически постоянной приложенной нагрузки и контактных напряжений такое поведение e (t) является следствием смены механизмов пластической деформации и выноса материала из-под индентора в зоне контакта.

Рис.6. Зависимости скорости относительной деформации e и активационного объема g от продолжительности контакта для некоторых материалов. Римскими цифрами обозначены различные стадии в процессе формирования отпечатка.

Силовая зависимость скорости погружения в координатах lg e· = f(s) имеет участки, близкие к линейным, что позволяет путем экстраполяции в точку s₀ = 0 определить эффективные значения начальной скорости деформации e₀ на каждой стадии при различных температурах Т. Зависимость lg e₀ = f(1/T) в некотором диапазоне температур (различном для разных материалов) также оказывается линейной. Все это дает право говорить о термоактивированном режиме деформации, протекающей в соответствии с аррениусовским уравнением e· = e₀ (exp(U – gs)/kТ) (здесь U - энтальпия активации, s - среднее действующее напряжение в контакте, g - активационный объем, т.е. объем материала, в котором происходит деформация в результате одной термической активации). Активационные объемы, полученные из наклонов зависимостей lg e· = f(s), имеют на начальных стадиях погружения очень низкие значения ~ 10^–3 нм³ (порядка одного атомного) для всех исследованных материалов (рис.6), что прямо свидетельствует о деформации за счет движения отдельных атомов. Опыты по влиянию всестороннего внешнего давления на скорость диффузии дают также значения g около 0.6ё0.7 от величины атомного объема. Разумеется, существуют и дислокационные механизмы пластичности, характеризующиеся малыми значениями g (например, переползание), однако они слишком “медленные” для того, чтобы обеспечить скорость относительной деформации e > 10³с^–1, реализующуюся на начальных стадиях внедрения.

По мере углубления индентора и перехода ко второй и последующим стадиям, когда динамическое значение Н начинает приближаться к статическому (t > 10-12 мс), g в ионных кристаллах увеличивается до значений 0.1 нм³ (рис.6). Это свидетельствует о преимущественно дислокационном механизме течения материала под индентором на поздних стадиях внедрения. Из результатов независимых экспериментов хорошо известно, что для дислокационной пластичности в ионных кристаллах характерны величины g в несколько сотен атомных объемов, что и наблюдается на заключительных стадиях внедрения индентора. Но в кристаллах Ge, Si и аморфных сплавах Co₅₀Fe₃₅B₁₅ величина g и на заключительной стадии составляет менее 10 атомных объемов. Существует также много других свидетельств значительной роли точечных дефектов при локальном деформировании, полученных независимыми (правда, чисто качественными) методами [15, 16]. В ионных кристаллах переход от первой стадии погружения индентора ко второй наряду с быстрым увеличением g сопровождается сильным ростом U и плотности поглощаемой энергии. Схематическое изображение смены доминирующих механизмов деформации при формировании отпечатка представлено на рис.7. Здесь отдельная зона отведена точечным дефектам особой конфигурации - краудионам (одномерным сгущениям в расположении атомов, когда лишний атом внедряется вдоль определенного кристаллографического направления).

Рис.7. Схема, иллюстрирующая смену механизмов массопереноса при динамическом наноиндентировании в кремнии и фториде лития. Штриховкой показаны области, где отпечаток формируется благодаря движению дефектов того или иного типа.

В совокупности данные о величине g и приросте глубины отпечатка Dh_iна каждой i-й стадии позволяют установить вклад различных микромеханизмов массопереноса на каждой из выявленных стадий и оценить долю объема DV_i/V₀, вытесненного при формировании отпечатка посредством того или иного микромеханизма пластической деформации (V₀ - установившееся значение объема отпечатка). Как следует из рис.8, даже при длительности контакта t >1 с значительную часть пластической деформации во всех исследованных материалах обеспечивают моно- или малоатомные микромеханизмы массопереноса. При t <10 мс доля дислокационных механизмов массопереноса под индентором сильно понижается и вряд ли превышает 50% даже в мягких кристаллах. На тех стадиях внедрения, когда точечные дефекты дают превалирующий вклад в пластическую деформацию, максимальная динамическая твердость H_d^max может многократно превышать статическую H_s.

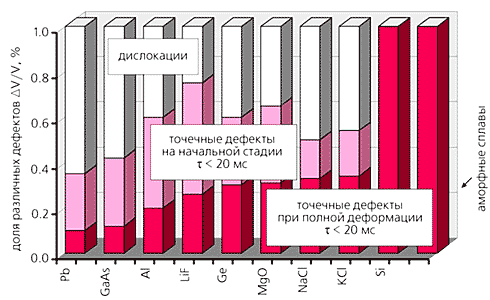
Рис.8. Роль точечных дефектов и дислокаций в массопереносе
при наноиндентировании для различных материалов.

Из приведенных данных вытекает, что с уменьшением продолжительности контактного взаимодействия и размеров отпечатка роль и вклад точечных дефектов возрастает, а дислокаций - падает. Поэтому анализ микроконтактной пластичности, возникающей во многих практически важных ситуациях, должен в большей степени опираться на представления о модах пластичности с участием точечных дефектов, нежели дислокаций. Завершая обсуждение динамики наноконтактов, укажем на неожиданную аналогию: поднятые проблемы до некоторой степени схожи с теми, которые возникли в космологии при анализе динамики расширяющейся Вселенной (та же сингулярность в “нуле” времени, те же изменения всех существенных параметров на много порядков величин, та же смена “эпох” по мере течения времени и роста характерных размеров задачи).

Отдельные замечательные главы в науке о наноконтактах - исследование электрических токов, спинового состояния и химических реакций в малой области поверхности, расположенной напротив близко стоящего атомарно острого зонда. В перспективе - это и наноэлектроника нового поколения (так называемая одноэлектроника, т.е. приборы, управляемые одним-единственным электроном), и нанолитография - высокоразрешающая технология локального химического модифицирования поверхности с целью получения сверхвысокой плотности элементов на кремниевой подложке, записи информации и многое другое. Но описание этих бурно развивающихся разделов физики нанаконтактов выходит за пределы объема статьи.

* * * Несмотря на значительное продвижение в понимании природы наноконтактов, достигнутое в последние годы, ряд принципиальных вопросов остается тем не менее открытым. Чем обусловлена смена механизмов массопереноса и пластической деформации по мере погружения индентора - изменением масштаба отпечатка и зоны деформации, течением времени, понижением действующих напряжений и скорости относительной деформации или необходимостью иметь большую концентрацию точечных дефектов для зарождения мелких дислокационных петель в условиях очень стесненной деформации? Каковы природа зависящей от времени части поглощаемой энергии в зоне деформации и механизмы восстановления отпечатка после разгрузки? И уж если помечтать, нельзя ли добиться в конце концов такого режима сверхскольжения, для которого трение бы вовсе отсутствовало, подобно отсутствию сопротивления при сверхпроводимости или сверхтекучести? Можно надеяться, что развитие прецизионных динамических методов нанотестирования позволит со временем ответить и на эти вопросы.

Работа выполнена при поддержке
Российского фонда фундаментальных исследований (проект 01-02-16573)
и Министерства образования РФ (проект E02-3.4-263).

Литература

1. Дедков Г.В. // УФН. 2000. Т.170. №6. С.585-618.

2. Bull S.J. // Wear. 1999. V.233-235. P.412-423.

3. Pethica J.B., Hutchings R., Oliver W.C. // Phil. Mag.A. 1983. V.48. №4. P.593-606.

4. Oliver W.C., Pharr G.M. // J. Mater. Res. 1992. V.7. №6. P.1564-1583.

5. Wolf B. // Cryst. Res. Technol. 2000. V.35. №4. P.377-399.

6. Bhushan B., Kulkarni A.V., Bonin W., Wyrobek J.T. // Phil. Mag. A. 1996. V.74. №5. P.1117-1128.

7. Булычев С.И., Алехин В.П. Испытание материалов непрерывным вдавливанием индентора. М., 1990.

8. Farber B.Ya., Orlov V.I., Heuer A.H. // Phys. Stat. Sol.(a). 1998. V.166. №1. P.115-126.

9. Головин Ю.И., Тюрин А.И. // Письма в ЖЭТФ. 1994. Т.60. №10. C.722-726.

10. Головин Ю.И., Тюрин А.И. // ФТТ. 1996. Т.38. №6. С.1812-1819.

11. Головин Ю.И., Тюрин А.И., Иволгин В.И., Коренков В.В. // Журн. техн. физики. 2000. Т. 70. №5. C.82-91.

12. Golovin Yu.I., Tyurin A.I., Farber B.Y. // J. Mater. Sci. 2002. V.37. P.895-904.

13. Golovin Yu.I., Tyurin A.I., Farber B.Ya. // Phil. Mag. A. 2002. V.82. №10. P.1857-1864.

14. Golovin Yu.I., Ivolgin V.I., Korenkov V.V. et al. // Phil. Mag. A. 2002. V.82. №10. P.2173-2177.

15. Rozhanskii V.N., Velednitskaya M.A. // Phys. Stat. Sol.(a). 1971. V.8. №2. P.551-564.

16. Akchurin M.Sh., Regel V.R. // Chemistry Reviews. 1998. V.23. Pt2. P.61-90.