VIVOS VOCO: В.В. Самарцев, Л.А. Рассветалов, М.И. Куркин, «Задержка света в пути... »

Задержка света в пути и
другие необычные явления в оптике

В.В. Самарцев, Л.А. Рассветалов, М.И. Куркин

Виталий Владимирович Самарцев, д.ф.-м.н., профессор,
зав. лаб. нелинейной оптики Казанского физико-технического научного центра РАН.

Леонид Александрович Рассветалов, д.т.н., профессор,
зав. кафедрой радиосистем Новгородского государственного университета им. Ярослава Мудрого.

Михаил Иванович Куркин, д.ф.-м.н., профессор, зав.
лаб. теор. физики Института физики металлов УрО РАН (Екатеринбург).

Единственное, чему научила меня моя долгая жизнь, что наша наука перед лицом реальности выглядит примитивно и по-детски наивно, - и все же это самое ценное, что у нас есть.

А.Эйнштейн

Первая часть нашего заголовка заимствована у статьи Э.Корнелла из “Nature” [1]. Такие интригующие названия на общедоступном языке - большая редкость для научных публикаций. Обычно они включают два-три специальных термина, которые, безусловно, делают заголовок компактнее, но для большинства читателей он превращается в заклинание. Все это понимают, но привычка так писать уже стала безусловным рефлексом. Мы тоже вначале хотели назвать свою статью: “Фотонное эхо и когерентная спектроскопия” (сокращенно ФЭКС). Это сплошь специальные термины, но именно так именуются симпозиумы, которые проводятся более 20 лет: ранее в СССР, а теперь - в России.

Первый такой симпозиум состоялся в Казани в 1973 г. Его организовал профессор У.Х.Копвиллем, предсказавший вместе с В.Р.Нагибаровым в 1963 г. фотонное эхо. Тогда они назвали его световым, чтобы отличать от сигналов эха в радиочастотном диапазоне. Потом, после перерыва, с 1981 г. ФЭКС стал собираться регулярно с периодичностью в четыре года. Председателем оргкомитета был академик Л.В.Келдыш, затем - академик К.К.Ребане, а теперь его возглавляет профессор В.В.Самарцев. Симпозиумы не ограничивались национальными рамками: так, в работе ФЭКС участвовали профессор Ч.М.Боуден (США) - известный специалист по квантовым компьютерам - и профессор С.Р.Хартман (США), обнаруживший долговременное фотонное эхо, на основе которого впоследствии были созданы процессоры для обработки оптических сигналов. Финансовую поддержку в проведении оказывали Российский фонд фундаментальных исследований, Минпромнауки РФ и Американское оптическое общество. Последний ФЭКС состоялся в Великом Новгороде в июне 2001 г. на базе Новгородского государственного университета им. Ярослава Мудрого. Он собрал более 100 участников, которые сделали около 100 докладов. Здесь мы постараемся популярно рассказать о предмете обсуждения на этих симпозиумах.

Эхо эху рознь

Самое трудное в таких случаях - не отпугнуть читателя первой фразой. Название “Фотонное эхо и когерентная спектроскопия” - не самое лучшее начало в этом смысле. Дело здесь не только в специальных терминах, но и в необычной трактовке понятия “эхо”. Действительно, поскольку в повседневной жизни под эхом мы понимаем звуковой сигнал, отраженный от препятствия, то фотонное эхо сразу ассоциируется с отраженным электромагнитным сигналом, т.е. попросту с радиолокацией. Такая трактовка вряд ли способна привлечь к нему внимание. Распространение этой аналогии на оптические фотоны позволит включить сюда лазерные прицелы, что могло бы заинтересовать профессиональных киллеров, если бы они читали журнал “Природа”. Есть еще одна возможность привлечь внимание публики к ФЭКС - заменить слово “фотонное” на “световое”, как было в первой работе Копвиллема и Нагибарова. Соответствующая аббревиатура позволяет достичь поставленной цели, но создает, как выяснилось, определенные трудности организаторам симпозиумов.

Получается, что словом “эхо”, если его понимать буквально, вряд ли можно заинтриговать читателя. Необходимо сразу же указать, что в физике понятие “эхо” расширено и включает в себя любой задержанный сигнал. При таком определении механизм формирования эхо-сигнала с помощью отражателя оказался не единственным, а главное - не самым эффективным, по крайней мере для электромагнитных сигналов, к которым относится и фотонное эхо. Поскольку скорость света c=300000 км/с, для достижения секундных задержек отражатель пришлось бы помещать на Луне. На ФЭКС обсуждаются свойства фотонного эха с временами задержки до нескольких часов. Установка для получения таких сигналов на основе отражения имела бы размеры величиной с орбиту Юпитера. Чтобы ужать ее до размеров лабораторного стола (рис.1), нужно было найти способ “остановить” оптический импульс в этом устройстве и извлечь его оттуда через несколько часов.

Рис.1. Аппаратура для исследований фотонного эха в Казанском физико-техническом институте.
Установка защищена экранирующей сеткой.

Забегая вперед, отметим, что это не та задержка света, которая обсуждалась в упомянутой статье Корнелла, но выглядит она не менее привлекательно. Более того, она позволяет сохранить оптический импульс вместе с записанной на нем информацией. На рис.2 приведены два изображения, заимствованные из статьи Кс. Шена и др. [2]. Одно из них - оригинал, другое - копия, воспроизведенная с помощью фотонного эха. Читателю предлагается самому решить, какое из них - оригинал.

Рис.2. Оригинал и его изображение, полученное с помощью долговременного стимулированного эха.
Запись осуществлена на оптических переходах ионов Eu³⁺ в кристалле Y₂SiO₅
с временем оптической памяти 3 ч.

Безотражательное эхо вокруг нас

Поднатужившись, мы смекнули, что этот раздел следует начать с пожелания Эйнштейна: “Все должно быть изложено так просто, как только возможно, но не проще”. Обычно простое изложение получается в тех случаях, когда обсуждаемому явлению удается найти аналог в повседневной жизни. Для безотражательного эха таким аналогом может служить следующий пример. Представим себе забег на длинную дистанцию. Сразу после старта все бегуны бегут плотной кучей, т.е. имеют, говоря по-научному, близкие значения пространственных координат. Однако со временем наиболее тренированные бегуны уйдут вперед, а любители нарушать спортивный режим отстанут, и различия в их координатах станут заметными. Но тут выясняется, что старт был дан не в ту сторону. Следует команда “кругом”, после которой бегуны продолжат свой путь в противоположном направлении, так что наиболее быстрые из них окажутся в положении догоняющих. Допустим, что соотношение скоростей участников забега после такой команды сохранится, тогда через время, равное интервалу от момента старта до команды “кругом”, они все дружно пересекут линию старта, т.е. будут иметь одинаковые значения координаты относительно этой линии.

Теперь опишем этот же эпизод, но по-научному. При кучном перемещении можно говорить о согласованности движения бегунов. Однако по давней традиции русские слова в научной терминологии принято заменять иностранными, чаще всего английскими. Но с английским языком есть проблемы, на которые обратил внимание еще немецкий писатель Курт Тухольский: этот язык состоит из одних иностранных слов, которые к тому же неправильно произносятся. Так вот, если взять английский вариант слова “согласованность” и произнести его правильно, то получится термин “когерентность”. Он-то и утвердился в русскоязычной литературе по оптике, а потому автоматически вошел в название ФЭКС. С точки зрения этого понятия описанный выше соревновательный процесс можно рассматривать как распад когерентности по координате до команды “кругом” и ее восстановление после.

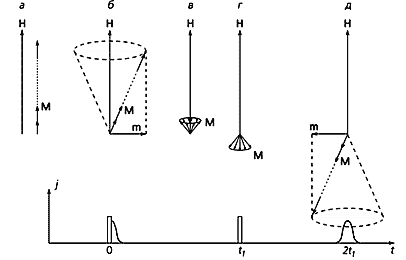
Рис.3. Схематическое изображение процессов, обеспечивающих формирование спинового эха.

Такого типа процесс распада и восстановления когерентности на более мелких объектах, магнитных моментах ядер, удалось реализовать в 1950 г. американцу Е.Хану [3]. Как всякие магнитные моменты их можно изобразить в виде векторов M, ориентированных вдоль магнитного поля H (рис.3,а). Стартовым сигналом для векторов M является импульс поперечного переменного магнитного поля, отклоняющий их от направления H (рис.3,б). Подобно наклонно поставленному волчку, прецессирующему вокруг вертикальной оси, наклоненные векторы M прецессируют вокруг H с так называемой частотой Лармора n, зависящей от величины H. На рис.3,б это движение символически изображено в виде конуса прецессии.

Сразу после стартового импульса векторы M параллельны, что соответствует когерентности их прецессий по фазе. Такая фазовая когерентность характеризуется суммарной компонентой намагниченности m, вращающейся вокруг поля H с частотой n. По законам электромагнетизма переменное магнитное поле, связанное с m, создает переменное электрическое поле, возбуждающее электрический ток в приемном устройстве.

Хан добился того, чтобы данный ток убывал со временем, что на рис.3,б изображено с помощью хвоста, следующего за стартовым импульсом. В эксперименте это достигалось за счет неоднородностей поля H, из-за которых частоты в разных точках образца оказывались разными. Поэтому векторы M, прецессируя с различными скоростями, в конце концов равномерно распределялись по поверхности конуса прецессии (рис.3,в). Получается хаотическое распределение фаз прецессий, т.е. фазовой когерентности нет. При такой взаимной ориентации векторов M переменная составляющая m=0, соответственно отсутствует и ток в приемнике.

При изменении знака поля H направление прецессии M меняется на противоположное, что соответствует команде “кругом” в рассмотренном выше примере. Технически это осуществляется с помощью импульса перемагничивания, который подается в момент времени t₁, когда фазовая когерентность потеряна (рис.3,г). После смены направления прецессии начинается восстановление фазовой когерентности. Она полностью восстановится через время t₁ после импульса перемагничивания, как и в случае примера с бегунами. Вместе с фазовой когерентностью восстановится и переменная составляющая намагниченности m, а следовательно, и сигнал в приемнике (рис.3,д). Именно этот сигнал Хан назвал спиновым эхом, поскольку он обусловлен ядерными спиновыми магнитными моментами. Его длительность определяется временем распада фазовой когерентности, т.е. длиной хвоста после стартового импульса.

В стартовом импульсе можно закодировать информацию, поэтому его обычно называют информационным. Импульсы перемагничивания (в спиновых процессорах их, как правило, несколько) удается приспособить для считывания информации или преобразования ее по заданной программе. В свое время это сулило бо?льшие перспективы для вычислительной техники по сравнению с ламповыми ЭВМ первых поколений, но конкуренцию с современной полупроводниковой техникой устройства на основе спинового эха не выдержали. Тем не менее методы, связанные с ядерным магнетизмом (так называемые методы ядерного магнитного резонанса - ЯМР) нашли широкое применение при изучении свойств различных материалов. В частности, ЯМР-томография считается одним из самых надежных методов медицинской диагностики.

Возбужденные атомы и плененные фотоны

Если вместо магнитных дипольных моментов ядер “привлечь к работе” дипольные электрические моменты атомов, аналогом спинового эха будет эхо фотонное. На первый взгляд различие между этими сигналами выглядит как чисто количественное. Частоты прецессий ядерных спинов лежат в радиочастотной области, соответствующей метровым радиоволнам, в то время как частоты колебаний дипольных электрических моментов атомов относятся к оптическому диапазону, т.е. выше в миллионы раз. Но с точки зрения квантовой механики это количественное различие приводит к качественному из-за того, что энергия оптического фотона (согласно формуле Планка E = hn, где h - постоянная Планка) в те же миллионы раз больше энергии радиочастотного фотона.

В случае спинового эха излучаемая энергия составляет ничтожную долю от полной энергии ядерных спинов, поэтому ее можно не учитывать при описании их поведения на всех этапах формирования эхо-сигнала. Энергетика фотонного эха выглядит совсем иначе. Достаточно сказать, что сами дипольные электрические моменты, на которых формируется эхо-сигнал, создаются стартовым импульсом. (Атом в “обычном” состоянии дипольным моментом не обладает, а приобретает его под действием внешнего электрического поля, переходя в возбужденное состояние.) Поэтому энергия поглощенного фотона не может быть меньше энергии других взаимодействий с участием возбужденного атома. Кстати, о поглощенных фотонах. Обычная модель с их исчезновением при поглощении не позволяет описать появление фотонов при излучении, когда атом “снимает” свое возбуждение. Более того, описание фотонов как объектов, движущихся со скоростью света, невозможно без использования специальной теории относительности. Раздел физики, объединивший квантовую механику и специальную теорию относительности, получил название квантовой электродинамики (сокращенно КЭД).

В КЭД электроны и фотоны не могут существовать раздельно. Каждый электрон обязательно окружен облаком фотонов, а каждый фотон - облаком из пар электрон-позитрон. Если быть последовательными, то в эту схему следовало бы включить другие элементарные частицы (барионы, мезоны, другие лептоны и т.д.), но такой выход за пределы КЭД в рамках одной статьи нам не одолеть. Здесь у нас нет возможности до конца разобраться даже с КЭД. Дело в том, что каждый фотон, имея равную нулю массу покоя, может существовать, лишь двигаясь со скоростью света. Именно по этой причине мы решили использовать словосочетание “задержка света” в названии статьи, надеясь хоть таким способом привлечь внимание читателей. Так вот, чтобы фотон не покинул пределы фотонного облака около электрона, он должен иметь возможность вернуться. Но как фотон может вернуться, если не в состоянии остановиться?

Решение этого парадокса нам придется отнести к know-how КЭД и дальше пользоваться ее готовым продуктом – представлением о плененных зарядами фотонах, существующих наряду с обычными свободными. Согласно этим представлениям размеры облака плененных фотонов сравнимы с их длиной волны l. Для оптических фотонов l ~ 0.5·10^–4 см, что в тысячи раз больше размеров атома. Можно оценить концентрацию возбужденных атомов, при которой их фотонные облака начнут перекрываться и процесс излучения фотона перестанет быть личным делом отдельного атома. Однако это не означает, что когерентная оптика начинается только при таком уровне оптического возбуждения среды. Есть и другие возможности добиться согласованности колебаний возбужденных атомов.

Фотоны плененные, но не сломленные

В атомной физике обычно имеют дело только с одним типом взаимодействия атомных электронов и свободных фотонов - поглощением фотона частоты n при переходе электрона из состояния с энергией E₁ в состояние с энергией E₂. Условием такого перехода является равенство:

n = n₀ = (E₂ – E₁)/h. (1)

При n № n₀ (для нерезонансных фотонов) такой переход также возможен, но время пребывания в возбужденном состоянии t оказывается конечным в соответствии с соотношением неопределенности энергия-время, которое относится к основным соотношениям квантовой механики:

(E₂ – E₁) t ~ h.

Из него следует, что время переизлучения нерезонансного фотона

t ~1 / |n – n₀| (2)

неограниченно растет по мере приближения к резонансу. КЭД ограничивает это время за счет эффекта спонтанного излучения фотона: время жизни возбужденного состояния атома оценивается как

t = t_m ~ (10^–8-10^–6) с. (3)

Учитывая, что размер атома r₀ ~10^–8 см, а скорость света в вакууме c = 3·10¹⁰cм/с, можно вычислить время пролета свободного фотона мимо атома:

t₀ = r₀/c = 10^–18 с (4)

и оценить, как изменится скорость света в веществе v, если этот фотон поглотится атомом, а затем переизлучится:

v = ct₀/t. (5)

Из формул (3) и (4) следует, что минимально возможная скорость света в веществе

v_min = c t₀/t_m ~ (1-0.01) см/с. (6)

На рис.4 представлена механическая модель распространения фотона в веществе с учетом переизлучения. Шарик массой m₀, двигаясь со скоростью v, налетает на цепочку сферических маятников, имеющих такую же массу m₀. При столкновении с первым маятником шарик, по законам упругих столкновений, передает ему всю скорость v. Тот совершает полный оборот (если v > 2(rg)^1/2, где r - длина подвеса, g - ускорение свободного падения) и после повторного столкновения с шариком возвращает ему скорость v. Далее шарик проделывает то же самое со вторым, третьим и последующими маятниками. Средняя скорость перемещения шарика определяется формулой (5), в которой под t₀ теперь следует понимать время прохождения шариком интервала между маятниками, t= t₀ + t₁ (t₁ - время оборота маятника), c = v.

Замедление распространения света в веществе - явление хорошо известное: с ним связан эффект преломления при переходе границы раздела двух сред. Его обычно характеризуют показателем преломления n (v = c/n). В обычных условиях значения n близки к единице (для стекла n около 1.5), в то время как из формулы (6) для v_min получается значение n=10¹². Что же мешает наблюдать значения n>>1 для резонансных фотонов?

Дело в том, что атомы в веществе участвуют в тепловом движении. Из-за этого их реакция на свободный фотон оказывается различной или, как принято говорить в оптике, некогерентной. В механической модели, изображенной на рис.4, такая некогерентность может быть связана, например, с выходом маятников из плоскости рисунка. В этом случае движение шарика станет непрямолинейным, и если вместо цепочки взять плоскую сетку маятников, то на выходе из нее шарик будет иметь произвольное направление скорости.

Рис.4. Механическая модель распространения света в веществе.

В оптике некогерентность движения атомов приводит к тому, что часть светового луча после прохождения через образец превращается в хаотическое тепловое излучение (эффект поглощения света веществом). Доля тепловых потерь возрастает по мере приближения частоты n к значению n₀ (1) (достаточно вспомнить темные фраунгоферовы линии в спектре Солнца, обусловленные поглощением света атомами в солнечной короне). Именно из-за сильного поглощения вблизи частот n₀ и не удается наблюдать замедления света, соответствующего n>>1, при обычных условиях. Другое дело, если бы можно было сделать движение атомов когерентным. В экспериментах, о которых идет речь в сенсационной статье Корнелла в “Nature”, это достигается с помощью дополнительного светового импульса. В такой специально приготовленной среде удалось наблюдать распространение светового импульса со скоростью 3·10³ см/с, что соответствует значению n = 10⁷. Хотя от предельного значения v_min = 0.01 см/с еще далеко, тем не менее результат впечатляет. Однако это все-таки не тот механизм задержки света, который обеспечивает существование фотонного эха.

Когда освобожденные из плена фотоны дают эхо

Итак, взаимодействие атомного электрона со свободным резонансным (n = n₀) фотоном может кончиться выселением первого в возбужденное состояние и задержанием второго. Но этот процесс занимает конечное время, в течение которого электрон блуждает между состояниями с энергиями E₁ и E₂, а задержанному фотону приказ об освобождении то подписывается, то отменяется. Если в промежутке между подписанием приказа и его отменой фотон успевает улизнуть за пределы фотонного облака, то попытка атома возбудиться оказывается неудачной. Таких сорвавшихся с крючка фотонов в образце обычно много, и связанное с ними результирующее излучение зависит от степени когерентности переходных процессов в атомах. Если они когерентные, то и излученные фотоны формируют когерентное излучение, подобное лазерному. Полностью некогерентные процессы приводят лишь к тепловому излучению.

Есть две причины, почему когерентное излучение имеет более высокую интенсивность по сравнению с тепловым.

Во-первых, когерентные фотоны максимально усиливают друг друга, поскольку их векторы электрического и магнитного полей параллельны. В случае тепловых фотонов эти поля имеют произвольную ориентацию, поэтому их среднее значение значительно меньше максимального.

Во-вторых, попадание когерентного фотона в фотонное облако возбужденного атома увеличивает вероятность излучения второго такого же фотона. Поэтому интенсивность вынужденного излучения гораздо выше, чем спонтанного, что и обеспечивает работу лазеров.

Теперь у нас все готово для описания процесса формирования фотонного эха под действием оптических когерентных импульсов. Первый когерентный импульс возбуждает в атомах переходные процессы, которые так же должны быть когерентными, по крайней мере первое время после импульса. Этим обусловлено активное последействие таких импульсов. Со временем когерентность разрушается, как и в случае спинового эха, что ведет к затуханию последействия. Однако с помощью специального второго оптического импульса, действующего подобно импульсу перемагничивания (рис.3), можно частично восстановить разрушенную когерентность. Тогда и возникает сигнал фотонного эха, аналогичного спиновому. Здесь уместно вспомнить, что на формирование фотонного эха отпущено время t < t_m = 10^–8-10^–6 с (3). Через это время все возбужденные атомы испустят хотя бы тепловой фотон и создавать фотонное эхо будет некому. Откуда же берется долговременное фотонное эхо с часовыми задержками, обнаруженное Хартманом?

Дело в том, что для атомов в кристалле набор возбужденных электронных состояний оказывается гораздо более разнообразным, чем у свободных атомов. В частности, возбужденный электрон может попасть в ловушку, из которой самостоятельно сможет выбраться только через несколько минут, а то и часов. Возможность образования таких ловушек недавно обсуждалась в “Природе” в связи с большими временами жизни конденсированного ридберговского вещества [4]. Для фотонного эха это оказывается важным, если второй оптический импульс обеспечивает не только восстановление когерентности переходных процессов в возбужденных атомах, но и забрасывает возбужденные электроны в ловушки. Оттуда их можно извлечь третьим, так называемым стимулирующим импульсом. После этого они включаются в переходные процессы и, восстанавливая когерентность, формируют сигнал фотонного эха (рис.5). Такое трехимпульсное фотонное эхо отделено от третьего импульса интервалом по времени не более 10^–6с. Но время задержки после второго импульса t₂ ограничено временем жизни электрона в ловушке, поэтому может длиться часами. Изображение на рис.2 получено с помощью фотонного эха от ионов Eu³⁺ в кристалле Y₂SiO₅ c временем оптической памяти 3 ч. Оказалось, что это не единственная польза от фотонного эха.

Эхо-голография

Под голографией обычно понимают фотографию, позволяющую создать объемное изображение объекта. Это достигается за счет интерференции луча, рассеянного объектом (объектного луча) с другим, так называемым опорным лучом. Соответствующая интерференционная картина будет определяться не только интенсивностью света, рассеянного данной точкой объекта, но и расстоянием от этой точки до опорного луча. Будучи запечатленной на тонкую фотопленку, эта картина и называется голограммой. Свет, рассеянный голограммой, после интерференции с другим опорным лучом дает объемное изображение объекта. Впервые такой способ записи объемных изображений был предложен и реализован в 1947 г. английским физиком Д.Габором. В 1962 г. советский ученый Ю.Н.Денисюк сумел осуществить запись толстых голограмм, которые позволяют получать объемные изображения без использования опорного луча.

Следующий шаг в развитии голографии осуществил американец Х.Геретсен, использовав для записи голограммы резонансные фотоны с частотой n₀ (1), взаимодействие с которыми увеличивает время жизни возбужденного состояния атома до 10^–8-10^–6с (3). Это дает возможность подавать объектный и опорный импульсы с задержкой по времени, на что в 1975 г. обратили внимание Е.И.Штырков и В.В.Самарцев. Однако экспериментально реализовать эту возможность удалось только в 1983 г. эстонским физикам А.Ребане, Р.Каарли, П.Саари. Подобный способ записи голограмм соответствует условиям формирования сигналов фотонного эха, что дало повод назвать данное направление эхо-голографией, хотя часто применяется также термин “пространственно-временная голография”. Сейчас профессор Ребане продолжает свои исследования в США. На ФЭКС-2001 он сделал доклад об использовании двухфотонных переходов при записи эхо-голограмм. Такие два фотона известны под названием “пара Эйнштейна-Розена-Подольского” (сокращенно ЭПР-пара). Есть соображения, что интерферограмма, записанная с помощью ЭПР-пар, позволит при воспроизведении образов использовать квантовомеханические свойства света.

Эффекты, обусловленные конденсацией возбужденных атомов

Обсуждавшаяся выше когерентность переходных процессов в атомах под действием фотонов поддерживалась (как в случае n>>1) или восстанавливалась (как в случае фотонного эха) за счет внешнего лазерного облучения. Имеется и другая возможность обеспечить подобную когерентность - уже за счет внутренних причин. Она возникает при достаточно высокой плотности возбужденных атомов, когда расстояния между ними R меньше длины волны излучения l:

R < l. (7)

При этом фотонные облака соседних атомов перекрываются и плененные фотоны обретают способность переходить от одного возбужденного атома к другому, становясь как бы их коллективной собственностью. Коллективизированные плененные фотоны не могут излучаться по одному, а только все сразу и, разумеется, когерентно. Этот эффект назвали сверхизлучением. С его помощью удается получать импульсы излучения, сравнимые по длительности с периодом световых колебаний T = 1/n = 10^–14c. Таким импульсам дали название фемтосекундных (1фс=10^–15с).

Для фотонного эха фемтосекундные импульсы представляют интерес в связи с усилиями по созданию оптических компьютеров, в которых в качестве носителей информации предполагается использовать оптические импульсы. Поскольку один наносекундный импульс (1нс=10^–9 с) можно составить из тысячи пикосекундных (1пс=10^–12 с) и миллиона фемтосекундных импульсов, использование последних для записи информации намного заманчивей.

Теперь обратим внимание на то, что возбужденные атомы, объединившие плененные ими фотоны, напоминают атомы в конденсированном веществе, объединившие свои валентные электроны. Используя эту аналогию, будем считать их конденсатом возбужденных атомов. Из-за когерентности плененных фотонов такой конденсат кроме сверхизлучения обладает еще и малым фотопоглощением, поскольку свету достаточно тратить свою интенсивность лишь на поддержание соответствующего уровня возбуждения среды. В электротехнике о проводниках со слабым поглощением говорят, что они обладают высокой электропроводностью. Аналогично можно говорить о высокой светопроводимости конденсата по сравнению с газом возбужденных атомов.

Экспериментально высокая светопроводимость конденсата проявляется в том, что возбужденные атомы имеют тенденцию “собираться” в нити с диаметром l, вытянутые по направлению распространения света. В результате свет распространяется не по всему сечению светопровода, а вдоль таких нитей конденсированной фазы возбужденных атомов. Похожий эффект в электротехнике называется шунтированием: при параллельном соединении двух проводников с разным сопротивлением ток предпочитает из них проводник с меньшим сопротивлением. Из-за малой толщины светопроводящих нитей, “суживающей” пучок света, эффект получил название самофокусировки.

Анализу структур, которые образуют такие нити, был посвящен доклад В.И.Юкалова из Дубны (Объединенный институт ядерных исследований). Ему удалось, во-первых, связать число светопроводящих нитей с геометрическими характеристиками светопровода. Во-вторых, найти критическое число этих нитей N_c, разделяющее два типа образуемых ими структур. При N<N_c в сечении светопровода нити образуют регулярную структуру, когда ближайшие расстояния между ними практически одинаковы. При N>N_c эти структуры становятся хаотическими. Эффект нарушения регулярности в расположении указанных нитей назван оптической турбулентностью.

Рис.5. Схематическое изображение световых сигналов при возбуждении долговременного фотонного эха с помощью трех импульсов (прямоугольники на схеме); t - интервал времени между первыми двумя импульсами; t₂ - интервал между вторым и третьим импульсами, длительность которого (оптическая память) может достигать нескольких часов.

Телепортация и телеклонирование с помощью света

Эти интригующие термины присутствовали в двух докладах, которые представили В.Н.Горбачев, А.И.Трубилко и А.И.Желиба из Санкт-Петербургского университета. Состоялась оживленная дискуссия, поскольку всем интересно было узнать, к чему эти явления ближе - к телевидению или к телепатии. Оказалось, что, с одной стороны, они выглядят проще телевидения, но с другой - столь же загадочны, как телепатия. Термином “телепортация” в упомянутых докладах названа процедура изготовления копии на значительном расстоянии от оригинала. Простейшим примером может служить пропускание лазерного излучения через два расположенных один за другим сосуда с газом из одинаковых атомов. Под действием света электроны в атомах возбуждаются. Если лазерный луч монохроматичен (имеет строго определенную частоту), то он вызывает электронные переходы только одного типа, так что все возбужденные атомы оказываются копиями друг друга. Таким образом, возбуждение атомов в удаленном сосуде подходит под определение “телепортация”.

Термином “телеклонирование” авторы назвали процедуру создания многих копий вдали от оригинала (множественная телепортация). В приведенном примере это соответствует случаю, когда в ближнем сосуде возбуждается один атом, а в удаленном - много. Разумеется, для описания одиночных возбужденных атомов использовать столь вычурную терминологию вряд ли целесообразно. В упомянутых докладах обсуждались гораздо более сложные многоатомные системы, но обязательно квантовые. Попробуем пояснить, зачем нужна квантовость.

Напомним, что состояние объекта в квантовой механике описывается волновой функцией (а не траекторией, как в механике Ньютона). Квадрат ее модуля имеет смысл плотности вероятности. В переводе с математического языка на человеческий, предыдущее предложение означает, что при измерениях одного и того же параметра квантового объекта могут получаться разные значения. Квантовая теория претендует на предсказание вероятностей получения каждого из этих значений. Но если речь идет о копировании, то всякое упоминание о вероятности представляется неуместным, так как копия должна быть неотличимой от оригинала, как говорится, на 100%. Таким образом, даже определение понятия “копия квантового объекта” оказывается нетривиальным.

Выручает здесь то, что волновая функция как решение соответствующего уравнения Шредингера всегда существует без всяких вероятностей. Следовательно, объект можно считать копией в буквальном смысле, если он и оригинал описываются неотличимыми волновыми функциями. Но дальше, если подвергать копию и оригинал измерениям, то появятся неоднозначности, описываемые вероятностными соотношениями. Квантовые объекты - необычайно хрупкие создания, поэтому любые воздействия, в том числе и связанные с измерениями, оставляют на них следы. Отсюда вывод, что при копировании квантового объекта изготовитель не должен пытаться выяснить детали его строения, так как после любой процедуры дознания получается, вообще говоря, другой объект.

Ситуация прямо-таки противоположная тому, с чем приходится иметь дело в повседневной жизни. Обычно, чем лучше знаешь устройство объекта, тем точнее получается копия. Впрочем, и здесь не обошлось без исключений. Пример - изготовление копий клеток и органов многоклеточных организмов. Эта процедура известна под названием “клонирование”. Несмотря на ограниченность наших знаний о биологии клетки, клонирование уже обсуждается на нормальном научном уровне.

Возвращаясь к телепортации, отметим, что в ней действуют два участника - отправитель (представитель объекта) и получатель (изготовитель копии). Мы сознательно не говорим о содержании отправления, так как ни отправитель, ни адресат не должны проявлять излишнего любопытства, чтобы не испортить копию.

Если говорить о технических приложениях телепортации и телеклонирования, то прежде всего следует упомянуть о квантовых компьютерах, для которых основная операция - приготовление объекта с заданной волновой функцией. Судя по недавно вышедшей книге [5], это направление сулит фантастические перспективы для информационной техники. Пока вопросы, связанные со статистической интерпретацией волновой функции в науке о квантовых компьютерах, не обсуждаются. Но когда до этого “дойдут руки”, телепортация и телеклонирование должны стать одним из ее разделов.

ФЭКС - наука фундаментальная или прикладная?

Мы упомянули только о наиболее интересных с нашей точки зрения достижениях тех разделов когерентной оптики, которые обсуждались на симпозиумах по ФЭКС. Конечно, они получены по крупицам в ходе длительных, рутинных исследований, составляющих кухню этой науки. Она представляет интерес только для специалистов. Гостей же обычно интересует не кухня, а сами блюда. Мы старались показать их с лучшей стороны, давая им оценку прежде всего с точки зрения полезности для оптических методов записи и обработки информации, оптических и квантовых компьютеров и т.д.* Возможно, мы перестарались, и у читателя возникла иллюзия, будто на ФЭКС говорят только о действующих или мыслимых деталях и узлах для таких устройств. Эта деятельность составляет содержание прикладных исследований, когда есть конкретная цель, план ее достижения и срок выполнения.

* И т.д. - сокращение, намекающее на то, что авторы знают больше, чем на самом деле.

Основная же часть докладов на ФЭКС была посвящена, как нам кажется, фундаментальным исследованиям. Вернер фон Браун так определил этот сорт научной деятельности: “Фундаментальные исследования – это то, чем я занимаюсь, когда понятия не имею о том, чем я занимаюсь”. Действительно, у такого исследования не может быть определенной цели, поскольку его результаты не должны быть предсказуемы. Вместо четкого плана используется метод проб и ошибок, причем ошибок оказывается гораздо больше, чем бы хотелось. О сроках даже говорить неприлично - “служенье муз не терпит суеты”. Тогда как отличить фундаментальное исследование от валяния дурака?

По-видимому, никак, пока не получится что-нибудь неожиданное. Когда же это происходит, такое валяние дурака уже называется фундаментальным исследованием. Мы надеемся, что РФФИ будет связывать ФЭКС с фундаментальными исследованиями и по-прежнему поддерживать симпозиумы этой серии. Мы заранее ему благодарны.

Литература

1. Cornell E.A. // Nature. 2001. V.409. P.461-462.

2. Shen X., Niguyen A. et al. // Science. 1997. V.278. P.96-100.

3. Hahn E.L. // Phys. Rev. 1950. V.80. P.580-584.

4. Маныкин Э.А., Ожован М.И., Полуэктов П.П. Конденсированное ридберговское вещество // Природа. 2001. №1. С.22-30.

5. Валиев К.А., Кокин А.А. Квантовые компьютеры: надежды и реальность. Москва; Ижевск, 2001.