VIVOS VOCO: Ю.Л.Войтеховский, "О кристаллах, полиэдрах, радиоляриях, вольвоксах, фуллеренах..."

О кристаллах,
полиэдрах, радиоляриях, вольвоксах, фуллеренах
и немного - о природе вещей

Ю.Л.Войтеховский

Юрий Леонидович Войтеховский, докт. геолого-минерал. наук, гл. научн. сотр. Геологического ин-та УрО РАН,
зав. лаб. Центра высоких технологий Кольского филиала Петрозаводского государственного ун-та.

Из студенческих лет память сохранила много забавных эпизодов. Однажды накануне Нового года в аудиторию буквально вбежал профессор кристаллографии И.И.Шафрановский. Кто его помнит, тот поймет, насколько странно было видеть очень пожилого, сгорбленного, обычно неторопливого маститого ученого столь возбужденным. Побегав вдоль доски, член нескольких зарубежных академий достал дрожащими руками из кармана пиджака листок белой бумаги и, развернув его, показал нам довольно симпатичную, явно вырезанную руками ребенка снежинку. “Посмотрите, какой ужас! Все ли видят, какой это ужас?”, - проскрипел своим характерным надтреснутым голосом Илларион Илларионович. И после длинной паузы, окинув печальным взором никак не отреагировавшую огромную холодную аудиторию и потрясая над головой бумажкой, профессор трагически произнес: “Вот как плохо учат наших внуков в детских садах! Запомните на всю жизнь - не бывает пятиугольных снежинок!”

Вторая история связана с именем столь же прославленного ученого - профессора минералогии Д.П.Григорьева. Что тут скрывать, мы его здорово побаивались. Уж больно строг был, хотя и справедлив. Байками про “ДэПэ” выпускники Ленинградского горного института до сих пор пугают молодых студентов-геологов. Зато экскурсии в Минералогический музей института и Эрмитаж, которые Дмитрий Павлович вдохновенно проводил для своих учеников, были незабываемыми. Как-то стоя с нами перед замечательной друзой горного хрусталя неподалеку от столь же уникальной глыбы малахита, Дмитрий Павлович заметил, что в фондах музея хранятся не менее красивые экспонаты. И на наш недоуменный вопрос, почему бы их не поставить вместо вон той невзрачной витрины с бокситами, ответил: “Как специалисты вы должны знать следующую правду. В жизни чаще встречаются серенькие и поцарапанные, а не яркие и сверкающие гранями кристаллы. Научитесь одинаково ценить и бриллиант в перстне, и мутное зерно кварца в граните, и чешуйку каолинита в скользкой после дождя глине”. Помня эти уроки, мне хочется рассказать еще одну правду, которая проясняется прямо на наших глазах и кажется мне важной.

Кристаллы и полиэдры

Речь пойдет о формах кристаллов, причем не каких-то экзотических, а самых обычных - в виде полиэдров (многогранников). Именно такими они вырастают в благоприятных условиях: при не очень больших пересыщениях питающих растворов, медленном изменении параметров среды, не теснимые соседями, не сотрясаемые подвижками земной коры... Естественная огранка кристаллов издревле поражала человеческое воображение. Поэтому ясно, что ее природа глубоко изучена. Кристаллография прочно стоит на геометрическом основании. При описании форм кристаллов удобным инструментом является теория симметрии. В зависимости от вида и числа осей, а также наличия плоскостей симметрии и центра инверсии кристаллы разделены на 7 сингоний и 32 класса. В каждом из них разрешены лишь определенные простые кристаллографические формы (всего 47), в сочетании образующие облик кристалла, если только он не искажен последующими процессами. Комбинации простых форм дают огромное теоретическое разнообразие вариантов. Специалистов давно интересует вопрос, какие из них встречаются в природе чаще. На сегодня установлено, что наиболее часты кристаллы планаксиального вида симметрии моноклинной и ромбической сингоний. Опуская подробности, поясним, что это не самые симметричные фигуры, хотя они достаточно далеки от форм тривиальных, вообще не содержащих элементов симметрии. Такой класс тоже имеется в систематике, хотя и выглядит изгоем перед лицом остальных, в которых есть хотя бы один, а чаще несколько замысловато взаимодействующих элементов симметрии.

Теоретически и фактически огромное разнообразие форм кристаллов подсказало мне идею рассмотреть их на фоне всего мыслимого многообразия полиэдров. И чтобы охватить их единым взглядом, нам не обойтись без некоторых упрощающих определений. Во-первых, под комбинаторным типом полиэдра далее будем понимать его совокупную характеристику, включающую число, тип (3-, 4-, ..., n-угольные) и способ соединения граней. Комбинаторный тип не меняется при непрерывной деформации полиэдра. Так, любой куб эквивалентен любому параллелепипеду. Во-вторых, под комбинаторной симметрией будем понимать симметрию самого симметричного полиэдра, имеющего тот же комбинаторный тип. Польза этих определений состоит в том, что если число различных полиэдров с данным числом граней (не меньше 4) бесконечно, то число их комбинаторных типов конечно и исчисляемо. При этом группа симметрии любого полиэдра (в зависимости от его конкретной метрической реализации) является некоторой подгруппой в группе комбинаторной симметрии. Иначе говоря, бесконечное разнообразие абстрактных полиэдров на уровне комбинаторных типов и симметрий становится обозримым и характеризуемым.

Систематическое перечисление комбинаторных типов полиэдров было начато английским математиком Т.П.Киркманом (1862), нашедшим все 4- ... 8-эдры. Наш соотечественник Е.С.Федоров (1893), заложивший основы теоретической кристаллографии, с помощью оригинального алгоритма перечислил все 4- ... 7-эдры, а также простые (в каждой вершине сходятся по три ребра) 8- и 9-эдры. Немец О.Гермес (1899), также независимо, нарисовал все 4- ... 8-эдры, а его земляк М.Брюкнер (1900) - простые 4- ... 10-эдры. Этим завершился “период рисования”, достоинством которого было всестороннее изучение каждой найденной формы. Но число полиэдров достигло такой величины, что ручной труд оказался далее невозможным. Прошло 65 лет, прежде чем к проблеме вернулись вооруженные компьютерами математики. Американец Д.У.Грейс (1965) пересчитал все простые 4- ... 11-эдры, его соотечественники Р.Боуэн и С.Фиск (1967) - простые 4- ... 12-эдры, голландец П.Дж.Федерико (1969, 1981) - все 9- и 10-эдры, наконец, швейцарец П.Энгель (1982, 1994) с помощью федоровского алгоритма нашел все 11-, 12- и простые 13-эдры. Я проверил данные о комбинаторных типах и симметриях всех 4- ... 10-, а также простых 11- ... 13-эдров, устранил некоторые ошибки и опубликовал изображения всех 4- ... 8- и простых 9- ... 12-эдров, поскольку - увы! - до сих пор самое лучшее описание полиэдра - его изображение. Для простых 13- … 15-эдров впервые найдена статистика точечных групп симметрии. Этим, в главных чертах, и характеризуется сегодняшнее состояние проблемы. Каковы же основные результаты по существу?

Все 4-, 5- и 6-эдры (1, 2 и 7 типов, соответственно) комбинаторно симметричны. Из 7-эдров (34) комбинаторно асимметричны 7 (рис.1), из 8-эдров (257) - 140, 9-эдров (2606) - 2111, 10-эдров (32 300) - 30 014, простых 11-эдров (1249) - 970, 12-эдров (7595) - 6756, 13-эдров (49 566) - 47 030, 14-эдров (339 722) - 331 796, 15-эдров (2 406 841) - 2 382 352. Тенденция очевидна - с ростом числа граней доля комбинаторно асимметричных полиэдров монотонно растет, достигая для 10-эдров в целом 93%, а для простых 15-эдров - 99%.

Рис. 1. Все комбинаторно асимметричные 7-эдры.
Никакой непрерывной деформацией нельзя получить из них симметричные формы.

Нас, конечно, интересует физическая интерпретация найденной закономерности. Однако здесь возникает сложность. По своей природе математика не является прислугой в доме естественных наук, но озабочена лишь собственной непротиворечивостью. И воистину достойно удивления, что всякая ее находка со временем обнаруживает адекватный природный объект. Впрочем, здесь внимательный читатель может заметить, что приведенная выше статистика точечных групп симметрии кристаллических полиэдров явно противоречит таковой для полиэдров абстрактных. Верно, но в последние годы благодаря применению сложнейшей аппаратуры ученые сумели проникнуть в мир микро- и наноразмерных минеральных индивидов. Оказалось, что подавляющее большинство открытых, что называется, “на кончике иглы” минеральных видов относится к низкосимметричным формам. Один из самых удачливых охотников за новыми минералами А.П.Хомяков прогнозирует изменение статистики в пользу низкосимметричных форм к 2005 г. По-видимому, природное многообразие кристаллов все же верно реализует главную потенцию нашего мира - довлеющее преобладание комбинаторно асимметричных форм.

Радиолярии

Изучение абстрактных полиэдров не только увлекательно само по себе, но и может принести практическую пользу. Поскольку не всякий читатель сочтет бесспорно полезным установленный факт асимптотического преобладания комбинаторно асимметричных форм над симметричными, я расскажу о полиэдрах, известных очень давно, но очевидная полезность которых обнаружилась совсем недавно.

В комбинаторной геометрии полиэдров есть замечательная теорема о том, что невозможен выпуклый полиэдр, у которого одновременно отсутствовали бы 3-, 4- и 5-угольные грани. Причем, если отсутствуют 3- и 4-угольные грани, то 5-угольных должно быть сразу не менее 12. Простейший пример - додекаэдр. Прелесть теоремы состоит в том, что она утверждает что-то важное о геометрических потенциях окружающего мира, которые нам даны и которые мы с легкостью не замечаем.

А можно ли разрешить наличие на полиэдре лишь 5- и 6-угольных граней? И еще потребовать для простоты представления, чтобы они сходились по три в каждой вершине. Оказывается, подобные формы уже изучал великий Л.Эйлер. И доказал, что у них должно быть ровно 12 5-угольных граней при сколь угодно большом числе 6-угольных! Правда, 13-эдры указанного типа невозможны. Это чуть-чуть уточняет теорему Л.Эйлера - первую из целого ряда теорем, характеризующих комбинаторное многообразие фуллеренов. Именно такое имя получили указанные гранные формы в дальнейшем. Однако обо всем - по порядку. Перенесемся назад во времени.

Вспомним рубеж XIX и XX вв. Бурный научный и промышленный прогресс. Мир упивается новыми техническими достижениями. Заводы, фабрики, автомобили, самолеты, корабли, радио, телефон… И рядом со всем этим почти незаметными остались научные океанографические экспедиции. Среди прочего, их результатом явилось первое микроскопическое исследование глубоководных илов, открывшее фантастический мир ажурных скелетов радиолярий, населяющих толщу Мирового океана. Благодаря Э.Геккелю, издавшему, кроме научных трудов, и красочные альбомы зарисовок, публика вскоре была зачарована невиданными картинами. В 1902 г. 18 брошюр под общим названием “Красота форм в природе”, содержащих 90 красочных таблиц, были изданы в Санкт-Петербурге товариществом “Просвещение”. Вы легко найдете среди них полиэдрические скелеты, явно относящиеся к фуллеренам или родственным им формам (рис.2).

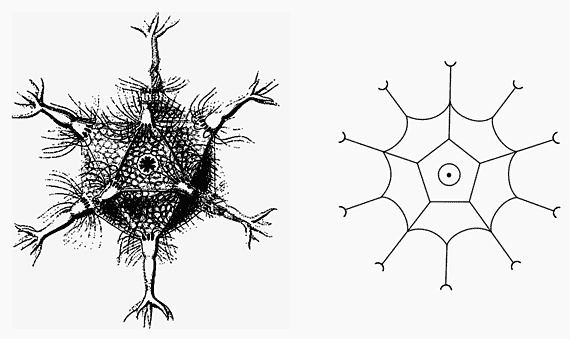
Рис. 2. Скелеты Circogonia icosahedra (слева, по Э.Геккелю), и C.dodecahedra (справа, по Д.Д.Мордухай-Болтовскому),
геометрически дуальные простейшему фуллерену - додекаэдру.

В 1936 г. советский математик и механик Д.Д.Мордухай-Болтовской в “Записках Ростовского государственного университета” опубликовал обширную работу под громким, но заслуживающим того названием “Геометрия радиолярий”. По систематичности и тщательности проработки проблемы она не превзойдена до сих пор. Впрочем, правильнее будет сказать, что она практически забыта вместе с именем автора. Для нас здесь важно то, что на рисунках среди прочих форм можно видеть все те же фуллерены (рис.2). Статья начинается словами “правильные формы в природе объясняются экономией материала”. К этой мысли мы еще вернемся.

“Ну и что из того, кроме красоты форм?” - спросит прагматично настроенный налогоплательщик. А то, что проблемы таксономии (классификации) и филогении (эволюционного родства) радиолярий далеко не исчерпаны. И если изучение сложных форм их скелетов хоть немного прояснит данные проблемы, то это позволит продвинуться в расчленении и корреляции разрезов погребенных и современных океанических осадков, реконструкции палеогеографических обстановок и, в конечном счете, прогнозировании минеральных ресурсов.

Вольвоксовые водоросли

Теперь мы плавно переместимся в смежную область. Примерно в то же время в прудах в окрестностях Харькова советский биолог А.Б.Коршиков изучал микроскопические колониальные зеленые водоросли семейства вольвоксовых. Было бы неправильно сказать, что до него ими никто не интересовался. Но его зарисовки были настолько детальными, что до сих пор кочуют буквально по всем соответствующим отечественным учебникам, каталогам и монографиям. По-видимому, именно благодаря ему удалось выяснить о видах Pandorina morum, Volvox aureus, V.polychlamys и V.globator следующее любопытное обстоятельство.

Они образуют колонии клеток в виде однослойных сфер диаметром от долей до нескольких миллиметров. При этом клетки так плотно скреплены плазмодесмами, тянущимися от ядра к ядру, что колонии при ближайшем рассмотрении оказываются полиэдрами. Теоретический расчет последних я провел лишь для колоний P.morum, образованных 16 клетками. Для них возможны всего три комбинаторно различные формы, две из которых - фуллерены. Один из фуллеренов не имеет плоскости симметрии и потому обладает энантиоморфным (зеркально-симметричным) двойником (рис.3). Аналогичный расчет для других колоний с числом клеток от 100 до 20 000 сталкивается с вычислительными трудностями, не преодолимыми за разумное время. Формотворчество природы поистине превосходит человеческие возможности!

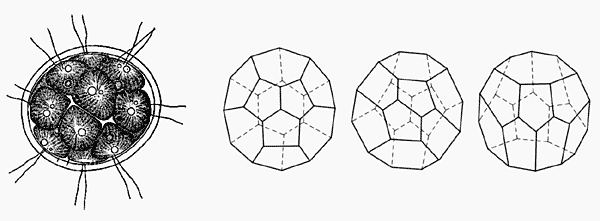
Рис. 3. Прорисовка реальной колонии Pandorina morum (слева, по А.Б.Коршикову),
и ее полиэдрическая интерпретация.

Человек, как известно, уже превратился в геологическую силу, большей частью разрушающую. И с помощью тех же водорослей мы пытаемся определить степень нашего воздействия на природу. Идея проста. Начиная с некоторого предела, морфологические особенности организма становятся чувствительными к отравлению среды обитания. Этот рубеж мы и надеемся установить для P.morum, анализируя частотный спектр их морфологических разновидностей при разных типах и интенсивностях загрязнений. Если это удастся, то мы получим новый индикатор экологического стресса. Параллельно попробуем определить биологическое разнообразие вольвоксовых. Заметим, что они широко распространены в южных и средних широтах нашей страны, а встречаются вплоть до Арктики. Это усиливает наш интерес к их возможной биоиндикаторной роли в районах интенсивной горнодобывающей, металлургической и сельскохозяйственной деятельности.

Самостоятельное значение имеет анализ распространенности в природе и биоиндикаторной роли энантиоморфов. Читателю наверняка известно, что в неорганическом мире такие двойники встречаются одинаково часто, а в мире органическом их распределение резко асимметрично. Например, закрученность всех молекул ДНК и почти всех раковин улиток в одну сторону. Эта проблема тесно связана с нашими представлениями о происхождении самой жизни. В разное время к ней обращались Л.Пастер, П.Кюри, В.И.Вернадский. Энантиоморфы P.morum - еще один удобный объект для исследования.

Фуллерены

А теперь перенесемся в совсем другую область - архитектуру. И вы уже догадались, там, где речь идет о гармонии, не обойтись без фуллеренов. Верно. Как, не прибегая к опорам, надежно и эстетично защитить крышей большие пространства? Например, футбольный стадион или выставочный зал. Этот вопрос волновал многих архитекторов. В 60-70-х годах прошлого века американца Р.Фуллера осенила идея строить полусферические купола с минимумом балок, обеспечивающих прочность конструкции. Как вы думаете, что получилось в результате многочисленных инженерных расчетов? Половинка огромного футбольного мяча, если представить его швы и кожаные лоскутки в виде балок и дырок. Сам же футбольный мяч есть все тот же фуллерен. Именно такой павильон выстроил Фуллер для Всемирной выставки ЭКСПО-67 в Монреале. Кстати, он любил спрашивать у своих коллег: “Сколько весит ваша конструкция?” Не правда ли, очень похоже на высказанную ранее мысль Мордухай-Болтовского об экономии материала в природных фуллеренах?

Теперь предлагаю заглянуть в астрофизику. В начале 80-х годов прошлого века американец Г.Крото изучал методами микроволновой спектроскопии состав газа в атмосферах звезд и межзвездных облаках. В атмосфере звезд-гигантов он обнаружил цепочечные молекулы, образованные атомами углерода и азота. В это же время англичане Р.Смолли и Р.Керл проводили исследования в кластерной химии с помощью аппарата, позволявшего превращать в плазму практически любое вещество. Счастливый случай свел их вместе. В 1985 г. был выполнен модельный эксперимент по лазерному испарению графита с его последующим охлаждением в сверхзвуковой струе гелия. Масс-спектрометрический анализ показал, что в продуктах преобладали кластеры с четным от 30 до 100 числом атомов, причем в подавляющем большинстве - С₆₀ и С₇₀.

Их структурный анализ составил самостоятельную проблему. Удалось установить, что полученный порошок растворяется в бензоле. И в согласии с известным химическим принципом - “похожее растворяется в похожем” - было решено, что в структуре кластеров принимают участие типичные для бензола 6-членные кольца. Но свойства порошка не походили на свойства известных кристаллических модификаций углерода: графита, алмаза и карбина. Родилась блестящая идея. А что, если замкнуть на себя плоскую графитовую сетку, составленную из 6-членных колец. При этом на полиэдре неизбежно возникали 5-членные кольца. Дальнейшие расчеты продемонстрировали, что физической стабильности подобных молекул способствуют как можно более высокая симметрия и как можно меньшее число контактов 5-членных колец. Такими простейшими формами, обладающими к тому же высокой симметрией, в полном согласии с экспериментом оказались полиэдры С₆₀ и С₇₀, которые выглядят как футбольный мяч! В честь Фуллера полиэдрические молекулы указанного типа назвали фуллеренами.

Заметим, что стабильность молекулы С₆₀ была предсказана японцем И.Осавой еще в 1970 г. Наши химики Д.А.Бочвар и Е.Г.Гальперн в 1973 г. подтвердили эту догадку необходимыми расчетами. Но экспериментаторы не проявили интереса к этим теоретическим работам. В результате Нобелевская премия по химии за экспериментальный синтез и расшифровку структуры фуллеренов была присуждена в 1996 г. Керлу, Крото и Смолли. В чем же значение открытия? Не в последнюю очередь в том, что фуллерены представляют собой новую стабильную форму углерода. А ведь сама наша жизнь так тесно с ним связана! Вскоре фуллерены нашли и в природе: фульгуритах (породах, расплавленных при ударе молнии) Колорадо и шунгитах (высокоуглеродистых породах спорного, скорее всего магматического и метаморфического генезиса) Северной Карелии. Но главное значение открытия, конечно, состоит в огромных перспективах, связанных с получением на основе фуллеренов множества современных материалов.

Судите сами. Установлено, что фуллерены могут присоединять другие элементы и комплексы внутри и снаружи полиэдра, а также на место отдельных атомов углерода. Получаемые классы соединений - эндоэдралы, экзоэдралы и металлокарбоны - обладают уникальными свойствами. Эндоэдралы рассматриваются как потенциальные коллекторы других элементов. Это могут быть вредные элементы, и мы получим экологически надежные хранилища нового поколения для токсичных и радиоактивных отходов. Это могут быть полезные элементы, и мы получим медицинские препараты нового типа. Экзоэдралы уже находят практическое применение. Опыты по их гидрогенизации позволили японцам создать экологически безвредные аккумуляторные батареи, при тех же габаритах запасающие в пять раз больше водорода, чем существующие металлогидридные никелевые.

Кристаллы, созданные на основе фуллерена С₆₀ с введением атомов щелочных металлов, обладают сверхпроводимостью при рекордно высоких температурах - 19-33 К. Из высших фуллеренов получают трубки с наноразмерными отверстиями. В эксперименте они охотно всасывали расплавленный свинец, образуя проволоку с естественным углеродным покрытием. Плотно прилегая друг к другу, такие трубки образуют многожильные кабели. Это материал даже не для микро-, а для наноэлектроники будущего. А еще растворы фуллеренов обладают нелинейными оптическими свойствами, что позволяет строить оптические затворы, предохраняющие от вредного излучения. А еще на основе фуллеренов создаются как сверхнизко-, так и сверхвысокотемпературные смазочные материалы и всевозможные полимеры с уникальными свойствами. А превращение фуллеренов в алмаз происходит при гораздо более мягких условиях экспериментального синтеза, чем превращение графита. И еще много-много других применений, составляющих так называемые высокие технологии, которые завтра станут обыденными.

Сегодня нам еще удается удерживать приоритет в теоретическом изучении комбинаторного разнообразия фуллеренов. Передо мной на экране компьютера генерируются, сравниваются, сортируются и характеризуются различными параметрами все более сложные фуллерены. Нами успешно ведется компьютерный поиск и исследование параметров наиболее симметричных, в особенности икосаэдрических, фуллеренов без контактирующих 5-угольных граней. Именно эти формы интересуют сейчас специалистов по синтезу, поскольку, как мы упоминали, они потенциально стабильны (рис.4).

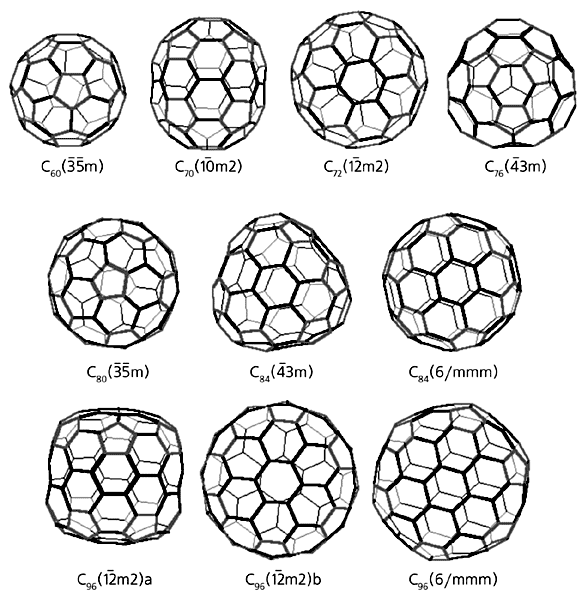
Рис. 4. Потенциально стабильные фуллерены диапазона С₆₀ - С₁₀₀.

Изучено полное комбинаторное многообразие фуллеренов вплоть до С₁₀₀, а икосаэдрических (с симметрией 3– 5– m и 235) - для любого числа образующих атомов. Результаты опубликованы в международных научных журналах. Как вы думаете, кто откликнулся первым и хотел бы тут же недорого купить компьютерные технологии? Китайские химики и турецкие биохимики. С сожалением приходится констатировать нерасторопность представителей отечественной промышленности.

Немного о природе вещей

Симметрия ассоциируется у любого человека с такими категориями, как соразмерность, пропорциональность, устойчивость, стабильность, гармония, надежность, предсказуемость, покой. Не потому ли для большинства из нас симметрия так притягательна? В этом смысле асимметрия - ее полная противоположность. Она волнует и беспокоит. Опираясь на данные естественных наук, можно сказать, что симметричные конфигурации структурных элементов на разных уровнях строения материи обычно более стабильны, чем асимметричные. Так, низкосимметричные минералы образуются, как правило, на заключительных стадиях геологического процесса и устойчивы в очень узком диапазоне условий. Иначе говоря, стабильные конфигурации - лишь временные, редкие остановки на пути вечного движения материи. Временная относительная устойчивость на фоне глобальной неустойчивости - вот правда о нашем мире. В частности, она проявляется и в довлеющем преобладании комбинаторно асимметричных полиэдров над симметричными. И, заметим попутно, наряду с теорией симметрии пришло время строить теорию асимметрии, определив ее позитивно и не рассматривая лишь как недосимметрию.

Недавно я провел эксперимент над высокообразованными коллегами, попросив назвать все известные им полиэдры. Выяснилось, что никто не назвал ни одной комбинаторно асимметричной формы. Иначе говоря, никто не знал нормы окружающего мира! Феномен объясняется просто. В раннем детстве мы играем кубиками и пирамидками. Наверное, это благоприятно действует на психику, ведь неустойчивая конструкция заставляет ребенка плакать. Но в школе, а затем и в университете, восхищаясь телами Платона, Архимеда, Каталани, Залгаллера, мы так и не выходим за пределы детского очарования симметричными формами. По-видимому, уже здесь на уровне подсознания формируется и незаметно транслируется во все сферы психики ошибочное представление о том, что устойчивость и предсказуемость есть норма бытия всего сущего в этом мире. Теоретическая физика давно рассталась с лапласовским детерминизмом. Но мы все еще болезненно реагируем на встречающиеся на жизненном пути неустойчивости. Мне кажется, здесь есть о чем задуматься.

И все же, если нам удается зафиксировать стабильную форму, то она, скорее всего, симметрична. Ярчайший пример - фуллерены. Знакомство с ними захватывает сразу. Здесь все поражает. И строгая красота, и целесообразность, опробованная природой и обществом в столь различных ипостасях: углеродистые фуллерены, скелеты радиолярий, колонии зеленых водорослей, мячи для футбола и регби, купола выставочных залов и многое другое. Предпосылкой этого служит бесконечное комбинаторное многообразие фуллеренов, заданное поразительно простыми исходными условиями. Природе и человеку есть из чего выбирать. Оптимальность конструкции будет достигнута при любом смещении параметров среды и социального заказа. При современной специализации науки за множеством единичных фактов мы подчас забываем о природе вещей, пока вдруг не наталкиваемся на феномен удивительный, подобный фуллеренам, сквозь который настойчиво просвечивают единство и красота мира. Согласитесь, ведь мы забыли, что изначально “космос” значил “красота”, и повседневно довольствуемся косметикой, т.е. украшательством.

Работа выполнена при поддержке Российского фонда фундаментальных исследований.
Проекты 94-05-16070 и 96-05-64203.