VIVOS VOCO: А.К.Звездин, "Квантовая механика плененных фотонов"

Квантовая механика плененных фотонов

Оптические микрорезонаторы, волноводы, фотонные кристаллы

А.К.Звездин

Анатолий Константинович Звездин, д.ф.-м.н., проф., гл. научн. сотр. теоротдела Ин-та общей физики им.А.М.Прохорова РАН.

Когда говорят о квантовой механике, в первую очередь возникают ассоциации, связанные с электроном: дуализм “волна—частица”, уравнение Шредингера, квантование уровней энергии электрона в атомах и т.д. Фотон (квант электромагнитного поля) находится как бы на втором плане. Безусловно, эта элементарная частица очень важна с концептуальной точки зрения, но в квантовой механике она рассматривается, главным образом, как промежуточный агент в задачах, где изучается взаимодействие излучения и вещества.

Состояние электрона может быть произвольным, как связанным (например, в атоме), так и свободным, и определяется внешними, действующими на электрон полями. Оно, точнее волновая функция электрона, вычисляется при помощи уравнения Шредингера, позволяющего найти энергетический спектр электрона (зависимость его энергии от импульса).

В отличие от электрона, фотон обычно считается свободной частицей с энергией E = ћw и импульсом p = ћk, где w — частота, k — волновой вектор (|k| = k = 2p/l, где l — длина волны), ћ — постоянная Планка. Энергетический спектр свободного фотона непрерывен (как и для свободного электрона) и характеризуется известным законом дисперсии электромагнитных волн

c = wk. (1)

Если фотон находится в прозрачном веществе с показателем преломления n, то вместо скорости света c в формулу (1) следует подставить u = c/n. Различие в поведении и описании электрона и фотона объясняется тем, что электрон обладает электрическим зарядом, поэтому на его состояние легко повлиять электромагнитным взаимодействием. Фотон в такой картине представляется как нечто, не поддающееся управлению и контролю при помощи внешних воздействий.

Как локализовать фотон?

Однако в конце XX в. ситуация с фотонами изменилась. Были созданы новые оптические материалы, структуры и приборы, в которых движение фотонов оказывается далеко не свободным, а весьма напоминает движение электронов в атомах, молекулах и кристаллах. Простейшая подобная структура — оптический микрорезонатор, т.е. полость, стенки которой обладают высоким коэффициентом отражения в определенном диапазоне частот. Очевидно, что движение фотона ограничено внутренним объемом полости. В англоязычной литературе такое свойство квантовой частицы обозначают словом “confinement”, т.е. “заключение в замкнутом пространстве”, или более кратко — “пленение”. Поэтому фотон, заключенный в микрорезонаторе, естественно называть плененным, или локализованным *. Как и у связанного электрона, у плененного фотона энергетический спектр становится дискретным.

* Проблема локализованных в пространстве фотонов издавна занимала классиков. Говорят, последним, начертанным рукой Бора на доске в его кабинете во дворце Карлсберг вечером накануне смерти (последовавшей 18 ноября 1962 г.), был чертеж эйнштейновского фотонного ящика, который имел непосредственное отношение к одной из главных проблем в дискуссиях Бора с Эйнштейном.

Близкими к микрорезонатору свойствами обладает, например, пленка или нить, состоящая из прозрачного материала с бо?льшим показателем преломления и окруженная средой с меньшим показателем преломления. На данном принципе основана волоконная оптика. Опять же по аналогии с электроном можно сказать, что среда с бо?льшим показателем преломления действует на фотон, как потенциальная яма на электрон, т.е. удерживает его в соответствующей области пространства.

Более сложная ситуация реализуется в новых искусственных оптических материалах — фотонных кристаллах. Этот термин ввел в научный обиход в 1987 г. Е.Яблонович [1], подчеркивая, что энергетический спектр фотона, движущегося в фотонном кристалле, аналогичен спектру электрона в реальном кристалле, например, в полупроводнике. Практически одновременно подобные результаты были опубликованы в работе С.Джона [2].

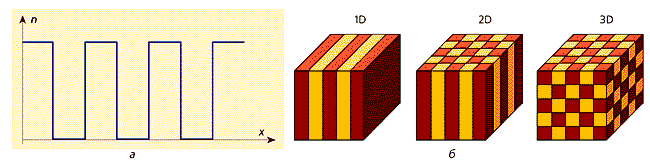
Рис.1. Зависимость показателя преломления от координаты (а) и схематическое изображение структуры фотонных кристаллов (б):
одномерного (1D), двухмерного (2D) и трехмерного (3D).

Фотонный кристалл представляет собой пространственно неоднородную структуру, характеризуемую периодической функцией n(x,y,z), где n — показатель преломления материала (рис.1,а). В целом картина напоминает потенциальный рельеф для электрона в кристалле. Здесь так же образуется запрещенная зона — определенная область частот, в которой запрещено свободное распространение фотона. Аналогия фотонный кристалл — полупроводник оказалась очень плодотворной для проектирования и создания новых оптических материалов и приборов, значительно расширивших возможности оптоэлектроники и информационных технологий. Справедливости ради нужно отметить, что еще в 1972 г. российский физик В.Быков из Института общей физики опубликовал ряд важных результатов, относящихся к подобным периодическим средам. Видимо, его работа и работы других авторов на эту тему были сделаны слишком рано, когда ситуация еще не созрела и внимание исследователей было сосредоточено на других, более актуальных тогда направлениях. Кроме того, немалую роль в буме, который инициирован работами [1, 2], сыграл броский термин “фотонный кристалл”. Еще знаменитый французский математик А.Пуанкаре заметил, что достаточно изобрести новое слово и это слово становится творцом.

Стимулировали интерес и практические нужды: свет привлекателен тем, что может нести очень большие потоки информации. Так, полоса частот оптоволоконного кабеля (~10¹² Гц) на много порядков превышает полосу частот электрического проводника того же диаметра. Другая интригующая перспектива — управлять интенсивностью спонтанного и индуцированного излучения атомов и молекул, находящихся в фотонных кристаллах или оптических микрорезонаторах, чтобы повысить эффективность разнообразных источников света: от лампочек накаливания до лазеров.

Заставить светить, а не греть

Хорошо известно, что при переходе электрона между уровнями энергии E_n и E_m происходит поглощение или испускание фотона. Вероятность такого процесса, например, процесса спонтанного испускания фотона, пропорциональна плотности фотонных состояний g(w) при частоте w = = (E_n – E_m)/ ћ. Грубо говоря, g(w) — это число фотонов, имеющих частоты в интервале от w до w + Dw, которые можно “поместить” в единице объема (1 см³). Для свободных фотонов плотность g(w) зависит только от частоты и равна (рис.2.)

g(w) = w² / (p²c³). (2)

Рис.2. Плотности состояний свободного фотона (1) и фотона, локализованного в 3D-микрорезонаторе (2).

Она определяет, в частности, интенсивность излучения тела, нагретого до температуры T (например, лампочки накаливания): интенсивность I(w) есть произведение энергии фотона ћw, числа возможных мест для него g(w) и соответствующей вероятности заполнения этих мест. Учитывая, что последняя задается функцией Планка, получим весьма низкую интенсивность источников видимого света, основанных на тепловом излучении (ламп накаливания и т.д.). Из рис.3 видно: даже при использовании наиболее жаропрочных вольфрамовых нитей (T ~ 2000°С) основная часть теплового излучения приходится на инфракрасный диапазон и только малая часть (~5%) попадает в видимый диапазон. Лампы накаливания в основном греют окружающее пространство, а не светят. Используя оптические микрорезонаторы и фотонные кристаллы, можно повысить световую отдачу и эффективность тепловых источников. В чем суть идеи?

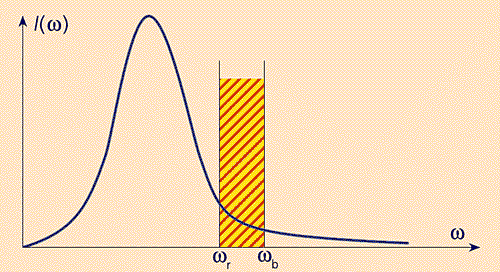
Рис. 3. Спектр интенсивности излучения I(w).
Заштрихованная область показывает часть полного распределения,
приходящуюся на видимый диапазон.

Если бы нам удалось так перераспределить плотность фотонных состояний g(w), чтобы она была максимальной в видимой области спектра и значительно меньшей (в идеале обратилась бы в 0) в ИК-диапазоне, то световая отдача, т.е. отношение световой энергии излучения к полной, существенно возросла бы. Управление геометрическими и физическими параметрами фотонных кристаллов и микрорезонаторов позволяет это сделать.

В простейших плоских оптических микрорезонаторах распространение фотона вдоль оси z ограничено металлическими зеркалами (рис.4,а) или так называемыми брэгговскими зеркалами (рис.4,б). Последние представляют собой системы чередующихся тонких диэлектрических слоев, сконструированных таким образом, чтобы за счет интерференции последовательно падающих и отраженных лучей полностью погасить прохождение света через зеркала. В качестве основного и вспомогательных слоев используют, например, полупроводники Ga_1-xAl_xAs с разным значением x; технология нанесения и согласования их между собой в последнее время хорошо отработана. Существуют 1D-микрорезонаторы — пленки, в которых есть одно запрещенное направление для распространения фотона, 2D-микрорезонаторы — оптические волокна, в которых запрещено свободное распространение фотонов в двух направлениях, и 3D-микрорезонаторы, в которых фотон полностью пленен (рис.1,б). В последнем случае уровни энергии фотона становятся дискретными.

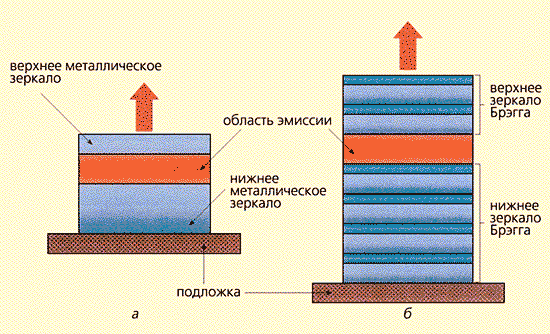
Рис. 4. Планарные микрорезонаторы:
с зеркальными стенками (а); с зеркалами Брэгга (б).

Пусть 3D-микрорезонатор имеет форму параллелепипеда с полностью отражающими стенками, тогда собственные частоты фотона в нем будут

w²_p,s,k = p²c²/n² ( p²/a²+s²/b² + k²/c²), (3)

где p, s, k — целые числа. Уровни энергии фотона в микрорезонаторе определяются как E²_p,s,k = = ћw²_p,s,k. Плотность фотонных состояний здесь — набор узких пиков, центрированных в точках w²_p,s,k (рис.2). Подбирая величины a, b, c, n (а также p, s, k), можно сделать плотность g(w) большой по величине (или, наоборот, почти равной нулю) в нужной области спектра. Этот факт был впервые обнародован в 1947 г. американским физиком Е.Перселлом и называется эффектом Перселла. Долгое время такая возможность управления спектром фотонов и вероятностью спонтанных переходов оставалась теоретическим предсказанием. В последние годы эффект Перселла был надежно экспериментально подтвержден.

Надо оговориться: полное отражение света не означает, что все излучение отражается на стенках. Действительно, фотон или пучок света, падающий из оптически плотной среды с показателем преломления n₁ на границу с оптически менее плотной средой с показателем преломления n₂ (n₂ < n₁) под углом, большим угла Брюстера q_B = arcsin n₂/n₁, испытывает полное внутреннее отражение. Но анализ уравнений Максвелла показывает, что при этом вместо прошедшей волны в оптически менее плотной среде вдоль поверхности распространяется так называемая латеральная, или побочная волна, амплитуда которой затухает как exp(–az), где z — расстояние по нормали от границы, a — параметр затухания. И если над поверхностью раздела сред поместить другую оптически плотную среду с n = n₁, латеральная волна проникает в нее и превращается там в свободно распространяющуюся волну с тем же волновым вектором, что и падающая волна в исходной среде.

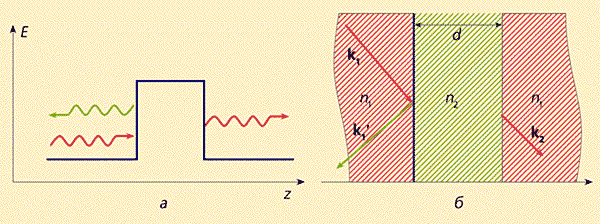
Рис. 5. Схематическое изображение туннелирования
электрона через потенциальный барьер (а)
и фотона через среду с пониженным значением показателя преломления (б).

Этот известный оптический эффект обычно интерпретируется в терминах квантового туннельного эффекта. Говорят, что фотон туннелирует из одной среды в другую так же, как электрон из одной потенциальной ямы в другую. Здесь аналогами потенциальных ям для фотонов, как отмечено выше, служат оптически плотные среды, а аналогом барьера между ними — оптически менее плотная среда (рис.5). Туннельный эффект фотонов широко используется в интегральной оптике для обеспечения оптической связи между различными оптическими каналами *.

* В действительности все происходило ровно наоборот. Сначала был обнаружен и исследован «туннельный эффект» в оптике. Это достижение принадлежит академику Л.И.Мандельштаму. Значительно позже (1927) он и его ученик, будущий академик М.А.Леонтович, распространили полученный результат на электроны. Термин «туннельный эффект» появился еще позднее.

Внутри фотонного кристалла

Для выяснения качественной стороны дела, так же, как это делается в физике твердого тела, рассмотрим одномерную цепочку оптических микрорезонаторов с расстоянием между ними, равным d, и расстоянием между центрами соседних микрорезонаторов, равным a.

Пусть E₁ и E₂ — два дискретных уровня, принадлежащих семейству разрешенных уровней резонатора. Предположим также, что фотоны, находящиеся в резонаторе, могут туннелировать в ближайшие соседние (левый и правый) резонаторы. Как это повлияет на уровни E₁ и E₂? В физике твердого тела ответ хорошо известен: дискретные уровни энергии E₁ и E₂ превращаются в разрешенные зоны, ширина которых увеличивается с увеличением амплитуды вероятности туннелирования (рис.6).

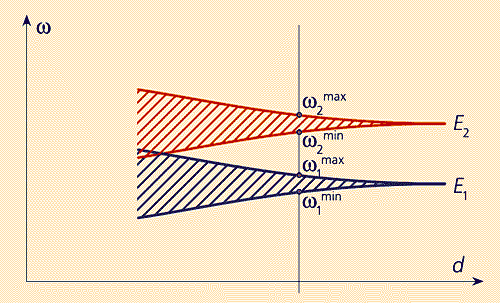
Рис. 6. Образование энергетических разрешенных полос из дискретных уровней w₁ и w₂ за счет туннельных переходов.

Если энергия фотона находится в разрешенной зоне, фотон свободно распространяется вдоль цепочки микрорезонаторов, хотя закон дисперсии, связывающий частоту и длину волны фотона, вообще говоря, кардинально отличается от такового для свободного фотона. Совсем необычно для оптики появление запрещенной зоны, наличие которой означает, что в данной области частот фотоны не могут свободно распространяться вдоль цепочки. Приведенные рассуждения естественно обобщаются на двух- и трехмерные структуры. Нужно лишь отметить, что расстояния между микрорезонаторами должны быть достаточно малыми и показатель преломления среды, заполняющей межрезонаторное пространство, также должен быть малым, чтобы в нем не могли находиться фотоны запрещенного диапазона частот.

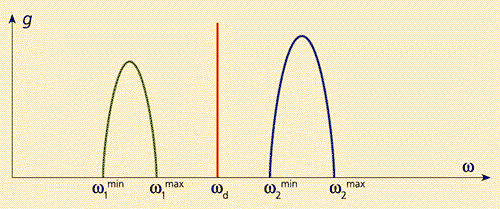
Рис. 7. Плотности фотонных состояний фотонного кристалла.
Область между w₁^max и w₂^min соответствует запрещенной зоне, а w_d — дефекту кристалла
(см. ниже рис.10).

На рис.7 схематически изображена плотность фотонных состояний g(w) для рассматриваемой модели. Ширина зоны тем больше, чем больше отношение n₁/n₂. Можно так подобрать период структуры и значения n₁ и n₂, чтобы запрещенная зона была в ИК-диапазоне, а в видимой области был бы пик плотности состояний фотонов. Такой фотонный кристалл станет идеальным материалом для теплового источника света. Особенно интересен в этом отношении металлический фотонный кристалл — периодическая структура из металла с высокой температурой плавления (например, вольфрама), погруженная в прозрачную диэлектрическую среду или воздух. Подобная система была недавно предложена независимо группой итальянских и российских исследователей из исследовательского центра ФИАТ и американскими учеными из лаборатории “Сандиа”. Согласно расчетам американских ученых [3], использование фотонного кристалла из вольфрама сможет повысить эффективность лампы накаливания с 5 до 60%. Это привело бы к колоссальной экономии энергии и средств, идущих на освещение, и вдобавок снизило бы экологическую нагрузку из-за бесполезного нагрева окружающей среды. Кроме того, управляя спонтанным излучением атомов и молекул, можно улучшить параметры оптоэлектронных источников и лазеров. Отметим еще интересный экспериментальный факт, обнаруженный исследователями из “Сандиа”: фотонный кристалл преобразует падающее ИК-излучение в видимый свет, что очень полезно для повышения эффективности солнечных элементов. Наконец, фотонный кристалл можно использовать в качестве широкополосного светового фильтра (рис.8).

Рис. 8. Частотная зависимость коэффициента отражения от фотонного кристалла [4].

В понятии о запрещенной зоне фотонного кристалла — центральном в данном рассуждении — есть некоторая тонкость. Как уже упоминалось, различают три вида фотонных кристаллов — 1D-, 2D- и 3D-кристаллы. Полная запрещенная зона для фотонов существует только в трехмерных фотонных кристаллах. Слово “полная” означает, что запрещенная зона реализуется для произвольных ориентаций волновых векторов, т.е. для фотонов, распространяющихся в произвольном направлении (рис.9,а). В двухмерных и одномерных фотонных кристаллах запрещенная зона существует только для фотонов, которые распространяются в некотором телесном угле, достаточно широком в первых и значительно меньшем во вторых (рис.9,б). Несмотря на “неполноценный” характер таких зон, они тоже интересны для приложений, поскольку обладают многими характерными особенностями полной запрещенной зоны.

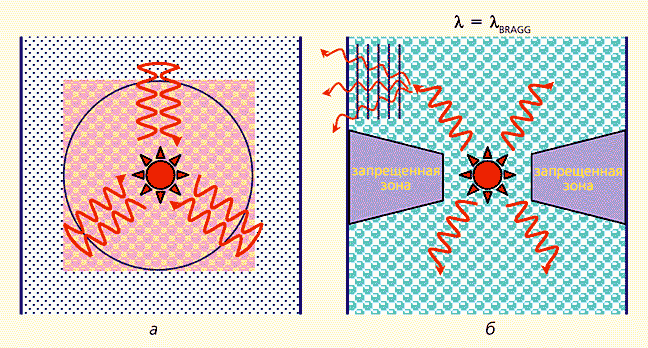
Рис. 9. Схематическое изображение процессов распространения света от точечного источника,
находящегося в фотонном кристалле с полной (а) и частичной (б) запрещенными зонами [5].

Известно, что дефекты в кристаллах, такие как вакансии, чужеродные атомы, дислокации, могут приводить к возникновению в запрещенной зоне разрешенных уровней. Подобным уровням соответствуют локализованные состояния электронов. Аналогичная ситуация реализуется и в фотонных кристаллах. В качестве дефектов также могут быть вакансии, т.е. пустые элементы в решетке, или элементы, заполненные материалом с другим коэффициентом преломления. Эти типы дефектов называют точечными, но на самом деле они — микрополости, или микрорезонаторы, которые могут захватывать или локализовывать фотоны и представляют большой интерес для создания эффективных точечных источников света, в частности лазеров с низким порогом генерации. Встречаются и линейные дефекты, в качестве которых, например, выступают нитевидные полости внутри фотонного кристалла. В отличие от точечных, линейные дефекты могут проводить вдоль себя свет (рис.10). Фактически они представляют собой оптические волноводы: даже если они сильно изогнуты, такие дефекты будут идеальными проводниками фотонов — они “ведут” свет без потерь! Не удивительно, что им оказывается столь большое внимание в технике оптической связи.

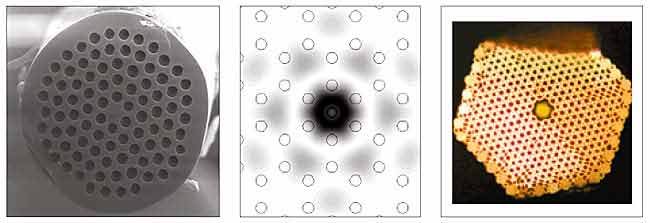
Рис. 10. 2D-фотонные кристаллы. Световедущие каналы и оптические волокна.

Аналогия между квантовым поведением электронов в полупроводниках и фотонов в кристаллах имеет строгое математическое обоснование: уравнения Максвелла после несложных преобразований могут быть представлены в виде, формально идентичном уравнению Шредингера для волновой функции электрона. Именно эта аналогия, на которую обратил внимание Яблонович [1], и стала источником многих идей в развитии физики фотонных кристаллов. Более того, оказалось, что процессы в фотонных кристаллах поддаются компьютерным расчетам со значительно более высокой степенью надежности, чем соответствующие задачи для электронов в кристалле. Это связано с одним из фундаментальных различий между фотонами и электронами — электроны обладают значительно более сильным взаимодействием между собой, чем фотоны. Поэтому “электронные” задачи требуют учета многоэлектронных эффектов, сильно увеличивающих размерность задачи, что заставляет часто использовать недостаточно контролируемые приближения, в то время как в фотонике данной трудности практически не существует.

Как делают фотонные кристаллы

Производство фотонных кристаллов для видимого диапазона длин волн (рис.11) — очень сложная проблема, так как постоянная решетки такого кристалла должна быть сравнима с длиной волны света, т.е. лежать в субмикронной области. Субмикронная область сейчас активно осваивается микроэлектроникой, основанной на планарной технологии, однако здесь речь идет о создании уже трехмерных периодических структур с субмикронным периодом. Напомним, что эта длина более чем в 100 раз меньше диаметра человеческого волоса. В настоящее время существует два пути производства фотонных кристаллов. Первый, называемый иногда сокращенно “сверху — вниз”, основан на литографии, широко используемой в микроэлектронике для производства полупроводниковых интегральных схем. Этот сложный метод, требующий очень дорогого оборудования, но в то же время очень точный и гибкий, позволяет в принципе создавать произвольные структуры и безусловно является перспективным. Здесь недавно были достигнуты впечатляющие результаты. К таковым относятся упомянутые выше металлические (вольфрамовые) фотонные кристаллы с очень широкой полной запрещенной зоной в диапазоне от 8 до 20 мкм. Период 3D-фотонного кристалла был равен 4.2 мкм, толщина элементов — 1.2 мкм. Чтобы создать фотонный кристалл с запрещенной зоной, непосредственно примыкающей к видимому диапазону, необходимо переходить в нанометровую область.

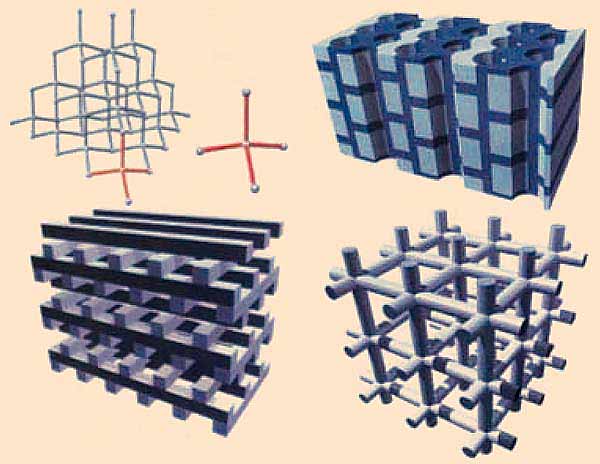
Рис. 11. Типичные структуры 3D-фотонных кристаллов [6].

Другой путь — “снизу — вверх”, основанный на спонтанной кристаллизации коллоидного раствора мелких частиц и называемый самосборкой, обеспечивает быстрый и сравнительно простой метод изготовления фотонных кристаллов. Метод самосборки применяется, главным образом, для создания диэлектрических фотонных кристаллов. Например, на первом этапе из коллоидного раствора методом самосборки из полимерных или кварцевых (SiO₂) микросфер выращивается трехмерная периодическая структура, которая используется далее как матрица для изготовления периодической оптической среды с заданными параметрами. На следующих стадиях пустоты матрицы заполняются материалом с высоким коэффициентом преломления, после чего микросферы удаляются путем химического травления, что и решает задачу.

К недостаткам метода нужно отнести малое разнообразие типов получаемых периодических структур (матриц). Кроме того, довольно трудно избавиться от случайных дефектов, которые “портят” запрещенную зону, но нелегко создать искусственные дефекты структуры, которые модифицируют зону нужным образом. Однако в последние годы Я.Власов и его коллеги из фирмы IBM доказали, что указанные препятствия могут быть преодолены [7]. Они вырастили крупные (размером порядка 1 см) и весьма совершенные фотонные кристаллы на поверхности кремния, отчетливо демонстрирующие наличие в них запрещенной зоны. Более того, ученые научились формировать в них искусственные дефекты. Все это, а также тот факт, что фотонные кристаллы выращены на поверхности кремния — основного материала микроэлектроники, очень обнадеживает. Тем более, что Природа уже поработала в данном направлении.

Недавно физики из Санкт-Петербурга и Минска [8] нашли интересные и глубокие аналогии в свойствах (поведении) фотонных кристаллов и естественного минерала — опала, который также состоит из плотно упакованных кварцевых сферических частиц, хотя и не обладает регулярной периодической структурой. Опалы издавна известны восхитительной игрой цветов, которая возникает, так же как и в фотонном кристалле, благодаря дифракции света на структуре кварцевых сфер.

Австралийские ученые из университета Сиднея открыли [9], что фотонные кристаллы встречаются в живом мире, а именно в морском черве, живущем в сравнительно глубоких морских водах. Морской червь покрыт “мехом” из иголок с яркой радужной окраской, которая переливается и играет в зависимости от угла падения света и угла наблюдения (рис.12,а,б,в).

Рис. 12. Морской червь Genus aphrodita (а), его радужные иголки (б, в)
и изображение поперечного сечения иголки в сканирующем электронном микроскопе (г).

Исследования с помощью сканирующего электронного микроскопа обнаружили у иголок наличие 2D-периодической структуры (рис.12,г), вероятно, с неполной запрещенной зоной. Здесь так же, как и в опале, игра цвета определяется дифракцией света на сложной микроструктуре, а не дисперсией коэффициентов поглощения и отражения на тех или иных красителях.

Некоторые бабочки (например, Morpho rhetenor, Южная Америка [10]) радужной окраской крыльев также обязаны дифракции света на микроструктуре чешуек их крыльев (рис.13).

Рис. 13. Бабочка Morpho rhetenor и детали выделенного участка ее крыла.

Эти открытия вдохновили исследователей из Марселя и Амстердама [10] на разработку новых видов тканей, окраска которых создается не только определенными пигментами, но и специально сконструированной микроструктурой; привлекают они и инженеров автомобильной промышленности. Оптические эффекты, характерные для 2D-фотонных кристаллов, можно поискать и в спектрах отражения шелковых ковров, изготовляемых искусными мастерицами из Керуана (Тунис). Плотность узлов в них порядка 10⁶ м^–2, и их цвет ярко и причудливо переливается на солнце при изменении угла падения света. Здесь дело, очевидно, тоже не только в пигменте, но и в дифракции света.

Но вернемся к проблемам фотоники. Если мы хотим обрабатывать информацию и передавать ее с помощью фотонов подобно тому, как это делают для нас электроны, надо научиться как-то фотонами управлять. Хотя электрического заряда у них нет, но наличие поляризации, т.е. ориентации их электромагнитного поля, дает определенную надежду на успех.

Путь к управлению поляризацией

С квантовомеханической точки зрения понятие поляризации света связано с наличием у фотона спина. Фотоны как частицы с нулевой массой покоя могут находиться в двух состояниях со значениями момента ±ћ, направленного вдоль импульса фотона; такие фотоны обладают круговой поляризацией: левой (квантовое число

m = +1) или правой (m = –1). Эллиптически поляризованные фотоны находятся в состоянии, которое складывается из состояний с m = ±1; при линейной поляризации суперпозиция этих состояний такова, что средняя проекция момента на направление импульса равна нулю.

Итак, фотон является двухуровневой системой, т.е. системой, описываемой квазиспином S_кв = 1/2, направление которого в пространстве определено полярным (a) и азимутальным (b) углами. Иными словами, множество состояний поляризации однозначно отображается на множество направлений, задаваемых углами a и b, или, что эквивалентно, на множество точек, принадлежащих некоторой сфере, которую в оптике называют сферой Пуанкаре, а в квантовой физике — сферой Блоха.

У свободного фотона состояния m = +1 и m = = –1 имеют одинаковые энергии (частоты). В квантовой механике такую ситуацию называют вырождением. Снять вырождение можно при помощи внешнего магнитного поля, направленного вдоль волнового вектора (предполагается, что фотон распространяется в среде с показателем преломления n): в поле компоненты с m = ±1 будут распространяться с разными скоростями:

u_± = (c/n)(1 ± Q). (4)

В результате в магнитном поле имеет место циркулярное двулучепреломление (гиротропия) среды. Магнитооптический параметр Q, в немагнитных средах пропорциональный магнитному полю, имеет типичное значение ~10^–6—10^–4. В магнитных материалах параметр Q отличен от нуля даже в отсутствие поля и достигает величин 10^–3—10^–1.

Экспериментально при этом наблюдается известный эффект Фарадея, т.е. вращение плоскости поляризации линейно поляризованного света при его распространении в среде вдоль магнитного поля. Угол его вращения (угол Фарадея) равен

q_F = (w/c)nQL = 2pLQ/l, (5)

где L — длина образца, l = c/wn — длина волны фотона в среде. Так ведет себя свободный фотон в магнитном поле.

Эффект Фарадея — один из наиболее эффективных методов управления свойствами фотонов. Он уже широко используется в лазерной технике, информатике и других областях [13] . Как он проявляется в случае плененных фотонов?

Поведение плененного фотона в магнитном поле существенно отличается от вышеописанного. Прежде всего заметим, что наличие геометрических рамок, ограничивающих движение фотона, уже само по себе, как правило, снимает вырождение состояний m = ±1 фотона. Рассмотрим, например, распространение фотона в тонкой пленке, состоящей из прозрачного материала с показателем преломления n. В этом случае состояния с m = ±1 расщепляются таким образом, что существуют

две различно поляризованные моды TE и TM, скорости распространения которых различны — u_TE и u_TM. В первой моде перпендикулярно направлению движения фотона направлено электрическое поле, во второй — магнитное. Электромагнитное поле в подобном волноводе можно представить в виде суперпозиции двух близких TE- и TM-мод.

Как и для свободного фотона, магнитное поле (или вектор намагниченности прозрачного магнитного материала), направленное вдоль волновода, вызывает переходы между модами. Например, если на “вход” прозрачного диэлектрического волновода поступает TE-мода, то из-за гиротропии, наведенной магнитным полем, она постепенно (по мере распространения) переходит в TM-моду (но обычно не полностью), затем обратно в TE-моду и т.д. Так реализуется эффект Фарадея в пленочном волноводе. Эффективность преобразования ограничивается, естественно, коэффициентом поглощения света и величиной расщепления TE- и TM-мод, т.е. разностью u_TE и uu_TM. Чем больше величина расщепления, тем меньше эффективность преобразования мод, т.е. тем меньше результирующая величина угла вращения плоскости поляризации света.

Аналогичный механизм эффекта Фарадея — конверсия TEЫTM-мод — реализуется в двухмерных фотонных кристаллах [11]. Как и в волноводах, чтобы достичь максимальной величины эффекта Фарадея (или максимальной эффективности управления светом), нужно согласовать TE- и TM-моды, т.е. сблизить их фазовые скорости.

В фотонных кристаллах возникает еще одна интересная возможность усилить эффект Фарадея. Как мы показали [11], для этого нужно “работать” на границе между разрешенной и запрещенной зонами, где происходит критическое замедление распространяющихся волн, что приводит к возрастанию соответствующих эффектов за счет увеличения времени взаимодействия волна—кристалл.

Квантовомеханическая аналогия

Обращает на себя внимание весьма близкая аналогия между рассмотренной картиной поведения фотона в волноводе и двухуровневой системой квантовой механики. Важной характеристикой двухуровневой системы является квазиспин S_кв (или вектор Блоха). Динамика Sкв определяется простым уравнением [12]:

¶S_кв/¶t = [S_квґ A_эф], (6)

где A_эф представляет собой эффективное поле, действующее на квантовую систему. Уравнение (6) описывает движение вектора S_кв по поверхности Блоха. Уравнение для квазиспина, описывающего фотон в волноводе или периодической среде, выглядит, как и (6), только вместо времени нужно использовать координату вдоль пути распространения фотона:

¶S_кв/¶x = [S_квґ F_эф(x)], (7)

где F_эф — эффективное поле, действующее на спин фотона. Разница заключается в том, что в квантовой электронике используются поля, зависящие

от времени, а в фотонике — от пространственных координат. Эта квантовомеханическая “спиновая” аналогия отмечена и обоснована в [13] примерно в то же время, что и аналогия Яблоновича, приведшая к созданию фотонных кристаллов. Логично ожидать, что квантовые эффекты, хорошо известные для двухуровневых систем, такие как нутация, p-импульс, эхо Хана и другие, имеют пространственные аналоги для фотона, распространяющегося в специально созданных пространственных структурах типа фотонных кристаллов. Так ли это на самом деле?

Уравнение (7) дает ключ к достижению максимальной эффективности преобразования мод в магнитных волноводах, подобно тому, как в квантовой электронике при помощи так называемого p-импульса решается аналогичная задача — обращение населенностей двухуровневой системы. Рассмотрим гармоническую модуляцию магнитного поля, существующую в волноводе (в магнитном материале подобную модуляцию можно создать, возбудив в нем стоячую магнитостатическую волну). Если длина волны модуляции a и разность волновых векторов TE- и TM-волн Dk согласованы, так что aDk = 2p, то вращение вектора Блоха по сфере (рис.14) происходит практически вдоль меридиана, и степень конверсии мод (или угол вращения Фарадея) линейно зависит от длины распространения волны. Для полной конверсии, например TE®TM, или наоборот, достаточна длина, при которой вектор S_кв переориентируется из северного полюса в южный, или наоборот, т.е. при угле переориентации S_кв, равном p. На практике обычно используют волноводы с чередующимся направлением намагниченности (рис.15), которые можно подобрать таким образом, чтобы достигнуть переориентации Sкв между северным и южным полюсами сферы (рис.14), т.е. с 100% конверсией мод.

Рис. 14. Изображение на сфере Пуанкаре процесса преобразования мод в волноводах с чередующимся изменением направления намагниченности. Пунктиром изображена траектория вектора Блоха для гармонического распределения намагниченности.

Есть здесь и аналог спинового эха. Американский физик Э.Хан, кому принадлежит честь открытия этого явления, предложил его образное объяснение. Пусть шеренга бегунов стартует на стадионе в момент времени t = 0, и дальше каждый бежит со своей, но постоянной, скоростью. Через некоторое время из-за разности скоростей шеренга рассыпается по беговой дорожке. Если в момент времени t подать сигнал, по которому бегуны поворачиваются и бегут назад, то в момент времени 2t они снова соберутся в шеренгу на старте. Роль бегунов в спиновом резонансе играют спиновые моменты частиц, которые прецессируют (“бегут”) вокруг магнитного поля с несколько различными частотами. Спиновое эхо широко используется в квантовой электронике.

Рис. 15. Магнитооптические волноводы с чередующимся изменением направления намагниченности в волноводной пленке вдоль оси x (а) и вдоль осей x и z (б); стрелками показаны направления намагниченности.

Подобный эксперимент можно произвести с фотонами. Рассмотрим схему эксперимента, изображенную на рис.16,а. Элементы U и V — два одинаковых двупреломляющих кристалла равной толщины. Пусть на входе в среду U падает полихроматический пучок света, линейно поляризованный под углом 45° к осям x и y кристалла. На выходе из кристалла U каждая спектральная компонента пучка будет иметь в общем случае эллиптическую поляризацию. Весь световой пучок в целом будет деполяризован из-за дисперсии. Такое состояние поляризации аналогично полной потере макроскопического магнитного момента перед воздействием второго импульса в явлении эха Хана. Если оси кристалла V будут повернуты на 90° относительно осей кристалла U, то результатом распространения света во втором кристалле будет полное восстановление состояния поляризации света на выходе из кристалла V, т.е. полихроматический пучок будет вновь линейно поляризован.

Рис. 16. Геометрия эксперимента по наблюдению пространственного фотонного эха; общая схема (а), при использовании электрооптического кристалла (б) и на анизотропных оптических волноводах (в) [14].

Для наблюдения эффекта можно использовать и электрооптические кристаллы. Роль элементов U и V тогда могут играть отдельные участки одного и того же кристалла, если приложить к ним электрическое поле во взаимно перпендикулярных направлениях (рис.16,б). Аналогичный эффект возможен и в анизотропных оптических волноводах, в которых ТЕ- и ТМ-моды связаны между собой (рис.16,в). В случае оптических волноводов эффект будет ярко выражен из-за сильной дисперсии, и эксперимент можно проводить в узком спектральном диапазоне.

* * *

Хотелось бы закончить статью известным историческим анекдотом. Английская королева, познакомившись с открытиями Фарадея в области электромагнетизма, спросила его об их практической пользе. На это Фарадей ответил: “Ваше Величество, что мы можем сказать о будущих достижениях новорожденного?”

Область физики и технологии, о которой шла речь в статье, также находится еще в очень юном возрасте, однако ее бурный старт позволяет надеяться, что она подарит нам много ярких открытий и практических достижений.

Литература

1. Yablonovitch E. // Phys. Rev. Lett. 1987. V.58. P.2059—2062.

2. John S. // Phys. Rev. Lett. 1987. V.58. P.2486—2489.

3. Fleming J.B., Lin S.Y., El-Kady R., Biswas K.M. // Nature. 2002. V.417. P.52—55.

4. Vos W.L., Megens M., Kats C.M. van, Bцsecke P. // J. Phys. Cond. Matter. 1996. V.8. P.9503—9508.

5. Megens M., Wijnhoven G.J., Lagendijk A., Vos W.L. // J. Opt. Soc. Am. 1999. V.B16. P.1403—1408.

6. Yablonovitch E. // Scientific American. Dec. 2001. P.47—54.

7. Vlasov Y., Xiang-Zheng Bo, Strum J.C., Norris D.J. // Nature. V.414. P.289—293 (Nov.2001).

8. Petrov E.P., Bogomolov V.N., Kolosha I.I., Gaponenko S.V. // Phys. Rev. Lett. 1987. V.81. P.77—80.

9. http://www.physics.usyd,edu.au/-nicolae/seamouse.htm

10. Tayeb G., Enoch S., Gralak B. // Optics&Photonics News. V.14. ?2. P.38—43 (February 2003).

11. Звездин А.К. Краткие сообщения по физике ФИАН. 2002. Т.12. С.37—50.

12. Клышко Д.Н. Физические основы квантовой электроники. М., 1986.

13. Звездин А.К., Котов В.А. Магнитооптика тонких пленок. М., 1988; Zvezdin A.K., Kotov V.A. Modern magnetooptics and magnetooptical materials // IOP Publishing. 1997. Bristol and Filadelphia.

14. Ахмедиев Н.Н., Звездин А.К. // Оптика и спектроскопия. 1989. Т.65. С.487—489.