№1, 1998 г.

© В.И. Арнольд Статистика первых цифр степеней двойки и передел мира   В. И. Арнольд Доклад, прочитанный акад. В.И. Арнольдом в Университете Торонто (Канада) 9 июня 1997 г.

Первая цифра числа 2ⁿ бывает единицей примерно в 6 раз чаще, чем девяткой. Так же распредеделены первые цифры населений и площадей стран мира. Предлагаемое ниже объяснение этого факта приводит к большому количеству математических гипотез, часть из которых доказана, а часть лишь подтверждена компьютерными экспериментами и ожидает строгого доказательства.

Степени двойки

Последовательность первых цифр чисел 2ⁿ (n = 0, 1, 2,...) начинается с

1, 2, 4, 8, 1, 3, 6, 1, 2, 5, 1,...

Можно проверить, продолжив вычисление, что единицы составляют примерно 30% членов этой последовательности (а девятка — меньше 5%). Такое же распределение получается для последовательности первых цифр чисел 3ⁿ и вообще для почти любой геометрической прогрессии. (Очевидное исключение составляют лишь прогрессии со знаменателями 10, 10^1/2 и вообще 10^p/q, где p и q целые.)

Доказательство сформулированного удивительного утверждения получено Г.Вейлем почти 100 лет назад. Он доказал даже больше. Напомню, что каждое действительное число c можно представить единственным образом в виде суммы целого числа (называемого целой частью числа c) и дробной доли {c}, принадлежащей интервалу [0, 1]).

Теорема. Пусть x — иррациональное число. Тогда последовательность {nx} дробных долей чисел nx (n = 0, 1, 2,...) равномерно распределена на интервале (0, 1).

Это значит, что число значений n, 0 ? n < N, для которых дробная доля nx принадлежит любому фиксированному отрезку длиной a, поделенное на N, стремится к a при N, стремящемся к бесконечности.

Иными словами, рассмотрим движение точки по окружности, в котором точка в целые моменты времени (n) перескакивает вперед на (несоизмеримый с 2p) угол 2px (рис.1). Теорема утверждает, что время, проведенное движущейся точкой на любой дуге окружности, асимтотически (при большом времени наблюдения) пропорционально длине дуги (и не зависит ни от положения дуги на окружности, ни от начальной точки, ни даже от величины угла поворота).

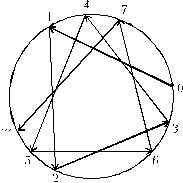
Рис. 1. Траектория точки при итерации проворота окружности

Распределение первых цифр чисел 2ⁿ получается теперь следующим образом. Рассмотрим последовательность чисел lg(2ⁿ) = nx. Число x = lg 2 иррационально (здесь и далее lg — логарифм по основанию 10). По теореме последовательность дробных долей чисел nx равномерно распределена на интервале (0, 1).

Но первая цифра i числа 2ⁿ определяется тем, в какой из интервалов между числами lg(i + 1) и lg( i ) попадает дробная доля числа lg(2ⁿ). По теореме, доли чисел 2ⁿ, начинающихся с i ( = 1, 2, ..., 9) составляют p_i = lg(i + 1) – lg i. Например, для первой цифры i = 1 эта доля составляет lg(2) = 0,301 (близость этого логарифма к 3/10 отражает близость 2¹⁰ = 1024 к 1000 = 10³. Поэтому доля единиц среди первых цифр чисел составляет примерно 30%. Доли всех цифр (в процентах) даются таблицей 1.

Табл. 1

 

Девяток примерно в 6 раз меньше, чем единиц (рис.2).

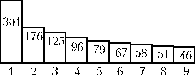
Рис. 2. Распределение первых цифр степени двойки

Из всего сказанного для дальнейшего важен такой вывод: приведенное в таблице странно неравномерное распределение первых цифр чисел последовательности объясняется равномерным распределением дробных долей логарифмов чисел нашей последовательности.

Этот вывод приводит к одинаковому распределению первых цифр для многих различных последовательностей (например, для геометрических прогрессий или , но не только для них).

Население стран мира

Лет двадцать назад Н.Н.Константинов сообщил мне, что первые цифры населений стран мира распределены так же, как первые цифры степеней двойки (табл. 2).

Табл. 2

Вот мое тогдашнее объяснение этого факта.

Согласно теории Мальтуса, население каждой страны растет в геометрической прогрессии. Из теоремы Вейля (см. предыдущий раздел) следует, что первые цифры населения фиксированной страны в последовательные годы распределены как первые цифры степеней двойки (см. рис.2). Согласно “эргодической теореме” (или, лучше сказать, согласно эргодическому принципу), временное среднее можно заменить пространственным: распределение по странам в один и тот же год должно совпадать с распределением в одной стране в разные годы.

Для контроля теории я рассмотрел числа страниц в книгах моей библиотеки, длины рек и высоты гор. Во всех этих случаях доли единиц и доли девяток среди первых цифр полученных чисел оказались практически одинаковыми: p_i = 1/9. Книги, реки и горы не растут в геометрической прогрессии, теория Мальтуса к ним не применима. Поэтому различие статистик первых цифр в числах, выражающих населения и, скажем, длины рек, служит своеобразным косвенным подтверждением формулы Мальтуса (согласно которой население растет в геометрической прогрессии).

Однако лет десять назад М.Б.Севрюк обнаружил, что не только населения, но и площади стран мира подчиняются такому же закону распределения первых цифр, как степени двойки! К площадям теория Мальтуса, по-видимому, неприменима, так что возник вопрос — как объяснить это поведение площадей. Ниже я пытаюсь дать ответ на этот вопрос.

Площади стран мира

Предыдущие примеры подсказывают, что следует искать причину странного распределения первых цифр площадей стран мира либо в их росте, либо в убывании (в геометрической прогрессии). История мира показывает, что площади стран (особенно империй) иногда растут, а иногда убывают за счет то присоединения одних стран к другим, то распада. Рассмотрим вначале самую примитивную модель этого явления. Предположим, что за единицу времени страна с вероятностью половина делится пополам, а с вероятностью половина присоединяет к себе другую страну такой же площади, как она сама.

Теорема. Распределение дробных долей логарифмов площадей, занимаемых такой случайной страной в момент n, стремится к равномерному распределению на интервале
(0, 1) при n, стремящемся к бесконечности.

Иными словами, вероятность того, что первая цифра площади окажется единицей, стремится при n ® ? к lg(2) = 0,3,01, ..., что она окажется девяткой — примерно к 0,046.

Действительно, рассмотрим последовательность l_n = lgS(n), где S — площадь в момент n. Точка в следующий момент n + 1 с одинаковой вероятностью сдвигается влево или вправо на lg 2 (причем, конечно, выбор, что делать — делиться или объединяться, — в каждый момент времени независим от выбора в другие моменты времени). По законам теории вероятностей, распределение величины l_n при больших n будет в основном сосредоточено на отрезке большой (порядка n^1/2) длины и будет пологим и симметричным (рис.3). При переходе к дробным долям (т.е. при “наматывании оси l на окружность l mod 1”) из такого распределения на оси l получится почти равномерное (при больших n) распределение на окружности (детали обоснования предоставляются читателю; важно, что последовательность дробных долей чисел mlg(2) распределена равномерно).

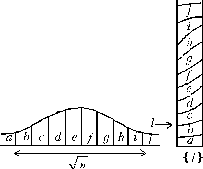
Рис. 3. При наматывании прямой с пологим распределением на окружность
на ней получается почти равномерное распределение.

Имеется множество более сложных моделей передела мира, приводящих в численных экспериментах к такому же эффекту. Вероятно, для целых классов таких моделей можно строго доказать предельную равномерность распределения дробных долей логарифмов площадей стран. Вот несколько примеров.

 
1. В начальный момент имеется k стран площадей S₁, ...,S_k . В каждый последующий момент одна (случайно выбираемая) страна с вероятностью 50% делится, а с вероятностью 50% объединяется с какой-либо (случайно выбранной) страной. Разумеется, выборы, делаемые в разные моменты времени, считаются независимыми и все случайно выбираемые страны равновероятны.

По вычислениям М.В.Хесиной (университет Торонто, июнь 1997) при S_i = i, k = 100 распределение первых цифр площадей стран становится практически таким же, как приведенное выше распределение первых цифр степеней двойки, уже через сотню шагов.

2. Введение деления на неравные части с каким-либо законом распределения частей (например, равномерным) приводит к такому же результату.

3. В моделях, где разрешается объединяться лишь с соседями, устанавливается такое же распределение первых цифр. Например, в одной из моделей Ф.Аикарди (Триест, июнь 1997) страны представлялись дугами окружности, а площади — длинами этих дуг. Распределение, практически неотличимое от распределения первых цифр степеней двойки, наступает очень быстро.

4. В другой модели Аикарди мир представляется графом, задающим разбиение сферы на треугольники (n вершин которых представляют n стран и снабжены “площадями”, распределенными на интервале (1, n) по закону случая). Граф строится, начиная с икосаэдра, при помощи итераций такой операции: случайно выбирается треугольная грань, добавляется вершина в ее центре и соединяется со всеми тремя вершинами грани.

Передел мира в этой модели организован так: в каждый момент (1,..., T ) выбирается случайно вершина i и затем с вероятностью p число стран увеличивается на 1 и
с вероятностью 1 – p уменьшается на 1. В первом случае случайно выбирается треугольная грань, содержащая эту вершину i, и вставляется новая вершина в центр грани. Затем эта вершина соединяется со всеми тремя вершинами грани и соответствующая вновь созданная страна получает от страны i долю ее площади (рис. 4).

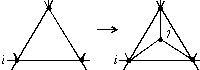
Рис. 4. Отделение новой страны j от страны i

Во втором случае случайно выбирается соседняя с i вершина j и затем страны i и j объединяются (причем на графе исчезает ребро ij и две разделенные им треугольные грани, рис. 5).

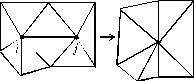
Рис. 5. Слияние стран j  и  i

В трех экспериментах A,B,C были выбраны следующие значения параметров (табл. 3).

Табл. 3

Средние (по 50 повторениям эксперимента с разными начальными условиями) значения долей единиц,..., девяток среди первых цифр площадей стран оказались такими (табл. 4; в последней строке (D) указаны частоты первых цифр степеней двойки).

Табл. 4

Было бы интересно не только доказать общую теорему, указывающую область применимости равномерного распределения дробных долей логарифмов, но и проверить, подчиняются ли этому распределению, например, размеры компаний и их доходы.

Появление странного распределения первых цифр во многих различных ситуациях неоднократно обсуждалось в литературе. Однако я нигде не встречал каких-либо математических теорем или гипотез (подобных приведенным в настоящей статье), обосновывающих неизбежность появления этого распределения (исключая, разумеется, теорему Вейля).

---

---

Октябрь 1999