Глава 2

ПЕРВАЯ КАПЛЯ ТАЛОЙ ВОДЫ

 

Что там творится в мире заоконном? Зима в исходе, видно по всему. Давайте вместе слушать, как со звоном Летит сосулька из зимы в весну. Александр Межиров

Капля, осушенная иглой

Расскажу об одном очень простом опыте, который когда-то в нашей лаборатории был поставлен и заснят на кинопленку. "Героем" фильма, естественно, была капля.

Начну с предыстории, с "общих соображений". Во многих учебниках физики утверждается, что жидкость смачивает твердое тело того же вещества: жидкая медь - твердую медь, вода - лед. Это означает, что если бы, например, на поверхности твердой меди поместить каплю жидкой меди, она должна была бы растечься по ней тонким слоем. Утверждается, что это веществу "выгодно", поскольку при этом его поверхностная энергия уменьшается, т. е. что поверхностная энергия твердой меди на границе с парами меди больше, чем сумма энергий на границе твердая медь - жидкая медь и жидкая медь - пары меди. Разумеется, медь - лишь пример. Имеется в виду, что утверждение справедливо применительно ко многим веществам.

Если авторы учебников физики не заблуждаются, то смачивание твердого тела жидким должно проявлять себя во многих явлениях. Ведь это означает выгодность наличия жидкой пленки на поверхности твердого тела. Чуть курьезно об этом можно сказать так: твердым телам выгодно быть мокрыми. Но окружающие нас твердые предметы сухи, если, разумеется, мы их специально не смочим. Впрочем, и смочить их не просто, так как смачивать надо жидкостью того же вещества, что и твердое тело, а такая жидкая пленка на твердом теле быстро кристаллизуется и, присоединившись к нему, становится твердой.

Впрочем, быть может, авторы учебников не заблуждаются и существуют условия, при которых потребность твердых тел быть мокрыми удовлетворяется. Ведь жидкая пленка на твердой поверхности - это как бы палка о двух концах. С одной стороны, пленка выгодна, так как с ее присутствием связано уменьшение поверхностной энергии, об этом уже говорилось. С другой стороны, пленка невыгодна, с ней связана избыточная "объемная" энергия: если пленка закристаллизуется, выделится энергия, и тем большая, чем дальше отстоит температура, при которой находится твердое тело, от температуры его плавления. Если дело обстоит так, то, быть может, авторы учебников все же правы и их правота не противоречит нашему жизненному опыту, протестующему против того, что якобы все твердые тела должны быть мокрыми. Быть может, твердые тела станут мокрыми, когда их температура непосредственно приблизится к температуре плавления, когда проигрыш "объемной" энергии будет меньшим, чем выигрыш "поверхностной". Ведь процессы, которые в природе происходят самопроизвольно, всегда движимы стремлением к уменьшению энергии. Скажем так: камень сам в гору не покатится, а вот с горы - при первой возможности.

В первые послевоенные годы в одном из томов "Докладов АН СССР" было опубликовано описание интересного опыта, который поставили В. И. Данилов и Д. С. Каменецкая. Опыт заключался в следующем. Маленький шарик металлического натрия, состоящий из нескольких кристалликов, медленно нагревался в ультратермостате, где температура поддерживалась и регулировалась с большой точностью, кажется, не меньшей пяти тысячных градуса. Границы между отдельными зернами на поверхности шарика очерчивались канавками. Они образовывали узор, подобный тому, который образуют швы на покрышке футбольного мяча. Канавки на шарике сохранялись при всех температурах, однако, когда до температуры плавления оставалось менее одной сотой градуса, они исчезали и вся поверхность шарика, ранее бывшая матовой, как бы покрывалась глазурью. Когда шарик натрия немного охлаждался, канавки снова появлялись, а затем повторным нагревом можно было заставить их исчезнуть, а поверхность покрыться глазурью. Это наблюдение легко объясняется "общими соображениями": жидкость смачивает собственное твердое тело, и поэтому вблизи температуры плавления твердое тело должно покрыться жидкой пленкой - она сглаживает канавки и придает поверхности блеск.

Авторы опыта с шариком натрия изучали не причины и закономерности появления и исчезновения канавок на его поверхности. Это наблюдение - побочный результат опыта, и поэтому они специально не стремились убедиться в том, что вблизи температуры плавления натрий запотевает, покрывается тонким жидким слоем.

Опыт, о котором рассказано, очень красив, но его результат лишь косвенно свидетельствует о правильности утверждения, что жидкость смачивает твердое тело того же вещества. Если жидкая пленка появляется, канавки должны исчезнуть, но не исключено, что они исчезают по каким-либо иным причинам, а причин может быть множество.

Здесь можно оставить предысторию и "общие соображения" и перейти к опыту, о котором говорилось в начале очерка. Мы пытались придумать прямой опыт, результат которого, не допуская кривотолков, убедил бы нас в том, что твердое тело с готовностью покроется жидкостью того же вещества, если такая возможность будет ему предоставлена. Вспомнили о ментоле - веществе, расплав которого очень легко переохлаждается. Кристаллики ментола плавятся при 35° С, но и при комнатной температуре ментол может оставаться жидким.

Рис. 12. Ментоловая капля наползает на кончик ментоловой иглы

Опыт заключался в следующем. На стеклянной пластинке поместили маленький кристалл ментола, подогрели его, расплавили, и он превратился в жидкую каплю. Ментоловая капля немного растеклась по стеклу и приняла форму плоской лепешки. Затем взяли ментоловую иголочку - продолговатый кристаллик ментола, сечение которого было много меньше площади капли, - и опустили ее в ментоловую переохлажденную жидкую каплю. Рассуждали так. Игла из кристаллика ментола может вмешаться в судьбу капли двумя различными способами. Она может явиться затравкой, которая вызовет кристаллизацию переохлажденной ментоловой капли. В этом случае капля, затвердев, останется на стекле в виде твердой лепешки, которая по форме мало отличается от формы жидкой капли. Может произойти и иное: ментоловая игла, оказавшись в непосредственном контакте с жидким ментолом, начнет жадно втягивать его на свои свободные поверхности, чтобы закрыть их жидкой пленкой. Если это произойдет, игла осушит каплю, как бы промокнет ее. Произошло именно это: у места контакта с каплей игла начала утолщаться. Дело обстояло так. Жидкий ментол, который в виде тонкого слоя наполз на поверхность иглы, кристаллизовался. На возникшую при этом свежую твердую поверхность опять наползал ментол и в свою очередь тоже кристаллизовался. Так происходило до тех пор, пока вся масса жидкой капли не перебралась на иглу. Разумеется, процессы наползания и кристаллизации не следовали один за другим, а происходили одновременно, но наползание было ведущим процессом. Нам, конечно, повезло: могла бы осуществиться первая возможность и капля осталась бы на стекле твердой лепешкой. В чем же причина везения? Главным образом в том, что наползал ментол на иглу со скоростью большей, чем кристаллизовался. Опыт с иным веществом, которое, как и ментол, подчиняется правилу, описанному в учебнике физики, окончился бы неудачей, если бы соотношение между скоростью наползания и кристаллизации было неблагоприятным для проявления наползания и капля отвердела бы прежде, чем заметная ее часть успеет наползти на иглу.

Обнаружив, что игла может осушить каплю, мы решили заснять этот процесс на киноленту и теперь показываем студентам двухминутный фильм на лекции, посвященной явлениям на границе между твердой и жидкой фазами. Кинограмма, иллюстрирующая очерк, смонтирована из кадров этого фильма.

Талая вода

Весеннюю капель, таяние снега, ручейки талой воды я почему-то всегда встречаю с грустью. Приход весны вызывает у меня ощущение не начала чего-то, а конца... Все свои планы я строю не на "учебный год" и не от новогодней ночи и до новогодней ночи, а от талой воды и до талой воды. Гонг, отбивающий годы, в моих ушах звучит весенней капелью.

Каждую весну я с грустью гляжу на талую воду. Много весен мелькало, но никогда я не задумывался над тем, как снег, белый и пушистый, рождает талую воду. Вопрос этот не возникал, видимо, потому, что ответ предполагался простым и давно известным: снег состоит из снежинок - кристалликов, эти кристаллики, как и все кристаллические тела, при определенной температуре плавятся, превращаясь в жидкость. Для снега эта "определенная температура" - нуль градусов. Вот и все.

Мне "по долгу службы" следовало бы больше знать об особенностях плавления снега. Снег ведь это не просто совокупность отдельных снежинок, каждая из которых ведет себя независимо. В снеге снежинки соприкасаются, образуя ажурную конструкцию из кристаллов и пустоты, а это, быть может, как-то влияет на судьбу отдельной снежинки. Быть может, капля воды рождается снегом не так, как снежинкой? Следовало бы знать, но я этого не знал, и лишь благодаря случаю пристальнее пригляделся к тому, как рождается талая вода - капля за каплей.

Я жил зимой в лесу, в небольшом деревянном домике. В отличие от сказочных лесных избушек, забытых богом и людьми, этот домик людьми не был забыт. Люди, персонал Дома отдыха, домик утеплили, установили в нем много батарей парового отопления и гнали по ним столько горячего пара, что в комнате было нестерпимо жарко. Температура воды в графине достигала, кажется, 30° С. Пить эту воду было неприятно, и я решил приготовить холодную воду - растопить снег и напиться талой воды. Вокруг домика было много свежего, сверкающего снега.

Здесь начинается рассказ о физическом опыте. Назовем его так: опыт первый. Прозрачный стеклянный стакан я доверху заполнил снегом, немного притрамбовал его и поставил в комнате на столе. Со временем снег опустился ниже кромки стакана и отстал от стекла. Минут через пятнадцать объем снега уменьшился почти вдвое. Снег терял белизну, в нем явно образовывалась вода, но на дне стакана ее не было - ни капли! Первые капли талой воды появились позже, когда снег, промокнув, начал в стакане расползаться, оседать.

Этот случайно поставленный опыт убедительно свидетельствовал о том, что, плавясь, снег удерживает в себе воду. Или лучше так: ту воду, которая раньше всего образуется на поверхности снега, где температура наиболее высока, снег всасывает в себя. Это удивительно напоминает осушение ментоловой капли ментоловой иглой. Вместо ментоловой иглы - пористый снег, в котором много поверхностей, "жаждущих" покрыться водой, вместо жидкого ментола - вода, образующаяся при плавлении поверхностного слоя снега.

Рис. 13. Последовательность кадров фильма о таянии снежных сфер

Первый случайный опыт мне показался нечистым, "упрекаемым", так как не все участки поверхности снега в стакане были в одинаковых условиях: боковая поверхность и верхний торец снежного цилиндра соприкасались с воздухом, а нижний торец, на котором цилиндрик стоял, - со стеклом стакана. Я поставил опыт преднамеренно - опыт второй. Из снега слепил небольшой шарик - такой, каким ребята играют в снежки. Продел сквозь него нитку и наблюдал за тем, что происходит со снежной сферой, прежде чем от нее отделится первая капля талой воды. Позже, уже в условиях лаборатории, этот опыт был повторен аккуратнее, со многими снежными сферами разных размеров, и все увиденное заснято кинокамерой. Чтобы результаты опытов можно было обработать количественно, рядом с шарами расположили масштабную линейку и часы. Кинолента рассказала о том, что со временем при комнатной температуре все снежные шары уменьшаются. Внизу каждого из них появляется вода, которая, однако, не капает, а остается в снегу. Снежная сфера со всех сторон равномерно обогревается воздухом, и вода появляется на всей ее поверхности. Капиллярными силами она втягивается в объем сферы, а затем под действием силы тяжести собирается в ее нижней части. Здесь сфера темнеет. Накапливающаяся вода продвигается к "макушке" сферы, и, когда весь объем сферы "напьется", от нее отделится первая капля. А затем капля за каплей - весь снег истечет талой водой. Чем меньше сфера, тем раньше появится первая капля. Немного простых рассуждений. Очевидно, перед рождением первой капли, насытившись водой, т. е. заполнив ею все поры, снежная сфера уменьшит свой объем на величину, равную объему пор. Объем пор равен произведению начального объема сферы на одинаковую для всех сфер величину пористости. Именно поэтому относительное изменение объема сферы до момента рождения первой капли не должно зависеть от ее начального размера. Ведь именно эта величина равна пористости. Из опытов и следовало, что относительное изменение объема снежной сферы не зависит от ее начального радиуса.

А теперь - немного стихов. Как-то мне попались на глаза такие строки о таянии снега:
 

...Что зима с землей ни делала, Как ни била, как ни жгла - Из-под снега, из-под белого Снова речка потекла...

Стихи эти складные, но очень неточно отражают процесс таяния: "из-под снега, из-под белого" талая вода не течет. А вот строки из стихотворения Николая Заболоцкого "Оттепель":
 

...Оттепель после метели. Только утихла пурга, Разом сугробы осели И потемнели снега...

Из-под такого снега талая вода вскоре появится, вначале - капля, а затем - бурный весенний поток.

Весенняя капель

Много физических явлений связано с весенней капелью. Например, можно рассказать о закономерностях образования изумительной по совершенству и красоте "каплевидной" формы капли, готовящейся оторваться от тающей сосульки. Не могу объяснить почему, но форма набухающей капли мне представляется верхом геометрического совершенства. Разве лишь сфера может сравниться с ней по красоте и логической законченности формы. Можно рассказать о солнечных бликах, живущих на поверхности капли, которая набухает на кончике сосульки. Блики колеблются в ритме дыхания набухающей капли. Можно рассказать о весеннем звоне, который, по мысли поэта, сопровождает полет сосульки из зимы в весну. Звон капели звучит во многих стихотворных и музыкальных строчках, и, конечно же, следовало бы рассказать об акустике удара капли о поверхность воды или льда, покрытого водяным слоем. Капля разбивается на мелкие осколки, и каждый из осколков вносит свое звучание в весенний звон.

Много физических явлений связано с весенней капелью, а здесь рассказ лишь об одном из них - о том, что происходит в тот момент, когда набухшая капля отрывается от родившей ее сосульки. Обычно глаз этого явления не замечает, точнее - в глаза оно не бросается. А кинокамера помогла сделать его зримым, очевидным.

Перед нами две кинограммы, смонтированные из кадров ленты, на которую был заснят процесс отрыва капли от двух различных сосулек, одна из которых - поострее, а другая - потупее. Первые кадры на этих кинограммах практически одинаковы. Они рассказывают о том, что набухающая капля увеличивает свой объем и, двигаясь по направлению к земле, вытягивает тонкую перемычку - связующее звено между сосулькой и каплей. Затем капля от перемычки отрывается и свободно падает, а оставшаяся перемычка начинает изменять свою форму. Она укорачивается, утолщается в нижней части и в виде сформировавшейся капельки отрывается от сосульки. Итак, рождению каждой крупной капли сопутствует рождение еще одной маленькой капельки. Ее объем существенно, приблизительно в 1000 раз, меньше объема первой капли, и, как правило, глаз ее не замечает.

Судьба маленькой капли оказывается очень неожиданной. Возникнув, она не летит вслед за падающей большой, а, наоборот, начинает двигаться вверх, по направлению к сосульке. Иногда это движение оканчивается тем, что малая капля достигает сосульки и как бы поглощается ею, а иной раз, немного переместившись вверх, она летит вниз вслед за большой.

Судьба маленькой капли зависит от того, какой толщины была перемычка, превратившаяся в капельку, а толщина перемычки зависит от того, насколько остра тающая сосулька. Капельки, возвращающиеся в сосульку, обычно рождаются сосульками остроконечными. Кинограммы потому и различаются последними кадрами, что они относятся к сосулькам с разным углом при вершине.

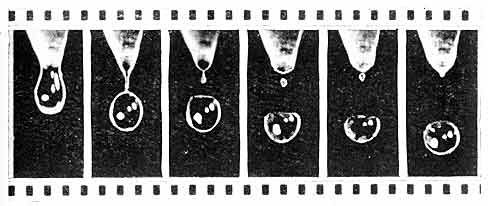
Рис. 14. Капелька, возникшая из перемычки, подпрыгнув, иногда возвращается к сосульке

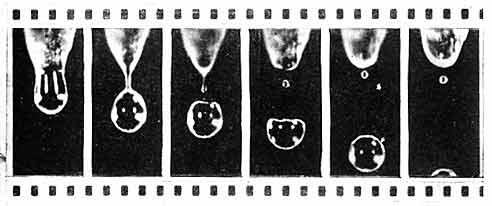
Рис. 15. А иногда она сосульки не достигает

Рис. 16. Из перемычки, соединяющей каплю и жидкость в пипетке,
образуется множество капель-сателлитов

Попытаемся понять то, о чем рассказывают кинограммы. После отрыва большой капли с перемычкой происходят два процесса: первый - на ее конце формируется маленькая капелька; второй - капиллярными силами эта капелька подталкивается вверх. Эти силы не возникли бы, если бы капля была обособленной, ограниченной сферической поверхностью. В такой капле было бы лишь скомпенсированное давление всестороннего сжатия. Капля на кончике сосульки вверху не закрывается сферической поверхностью, и поэтому к противоположному участку ее поверхности приложена нескомпенсированная сила, обусловленная лапласовским давлением Р_p; она-то и толкает каплю вверх. В тот момент, когда маленькая капля, сформировавшись, отрывается от сосульки, она еще продолжает двигаться вверх. Достигнет или не достигнет она сосульки, зависит от ее массы, от соотношения между силой, толкнувшей каплю вверх (F_up), и силой тяжести (F_dn), но некоторое движение вверх, как правило, наблюдается всегда.

Точно, с помощью формул, описать все происходящее с маленькой каплей очень непросто. Ограничимся приближенной оценкой. Сила, вынуждающая капельку падать вниз, определяется точно: F_dn = mg = 4/3 pR³rg. А вот силу, толкающую каплю вверх F_up, можно лишь грубо оценить, придав определенное значение диаметру перемычки, соединяющей капельку с сосулькой. Если R - радиус капли,  r - радиус перемычки, а Р_p = 2a/R, то F_up »  Р_ppr² = 2apr²/R. Чтобы капелька начала двигаться вверх, необходимо выполнение условия F_up > F_dn. Из этого условия следует, что R⁴ < 6ar²/4rg. Предположим, что R/r » 10. Разумеется, не точно 10, но такого порядка. В этом случае вверх заведомо полетит капелька, радиус которой удовлетворяет условию: R < 0,1 (6a/4rg)^1/2. Подставив в эту формулу значения констант (поверхностное натяжение a = 70 дин/см, плотность воды r = 1 г/см и g » 10 см/сек²), убедимся, что радиус капельки, летящей вверх, должен быть меньше, чем 0,3 мм. Именно такие капельки и запечатлены на кинограммах.

В заключение еще несколько слов о капельках, возникающих из перемычки, оставшейся после отрыва большой капли. Если источником большой капли является не конусная сосулька, а, скажем, плохо закрученный водопроводный кран или пипетка, может оказаться, что перемычка будет настолько длинной, что из нее образуется не одна, а несколько маленьких капелек. Эти капельки действительно наблюдаются. Оказывается, что та из них, которая ближе всех расположена к источнику воды, обязательно хоть немного движется вверх, а все остальные такой попытки не делают и следуют вниз за большой каплей. После рассказанного понять, почему так происходит, легко.

Пятна на столе

Эти пятна - укор неаккуратному фотографу. Они остаются на столе в фотокомнате, если, во-первых, манипуляции с растворами проявителя проводить небрежно, разбрызгивать их и, во-вторых, если после окончания работы тщательно не вытереть стол, на котором осталось множество капель этих растворов. Эти капли высыхают и оставляют после себя пятна. Можно, впрочем, пятна стереть, но прежде стоит пристально в них вглядеться - это не обычные пятна! Отчетливо видно, что при высыхании капли растворенные в ней соли осаждаются не равномерным слоем, а в виде последовательности чередующихся колец. Быть может, это свойство солей, применяющихся в фотографии, а не капель, и о них не стоит рассказывать в книжке, посвященной каплям? Давайте высушим раствор, нанесенный на стекло не в виде капли, а в виде равномерного тонкого слоя. Осадок есть, а колец нет! Значит, осадок в форме колец обусловлен тем, что высохла именно капля.

Чтобы проследить за тем, как образуется осадок в форме колец, процесс высыхания капель был заснят кинокамерой. Съемка производилась так. На предметном столике микроскопа - стеклышко, на нем - капля раствора сульфита, под ним - осветитель и слабый нагреватель, чтобы, подогрев стекло, можно было ускорить высыхание капли. На тубусе микроскопа - кинокамера, затвор которой автоматически щелкал каждые 30 сек. Съемку вели от момента, когда капля помещена на стекло, до ее полного высыхания.

Посмотрев ленту, можно убедиться в том, что капля высыхает скачкообразно. На обычных фотографиях эти скачки не видны, а на экране они видны великолепно. Вдоль периметра капли выпадают кристаллики осадка, и некоторое время диаметр капли остается неизменным. В какой-то момент он уменьшается, а затем стабилизируется, и вдоль периметра снова начинают выпадать кристаллики растворенной соли, образуя очередное кольцо в осадке.

Почему капля раствора высыхает так необычно? Казалось, терять бы ей постепенно влагу и так же постепенно уменьшать свой объем. Быть может, так и происходит? Объем уменьшается постепенно, монотонно, а скачкообразно, периодически изменяется форма капли?

Далее - рассказ об истинной причине скачкообразного перемещения периметра высыхающей капли. С каплей происходит следующее. Вода со всей ее поверхности испаряется равномерно (нет причин, чтобы этот процесс происходил как-то периодически). Легко понять, что по мере испарения влаги концентрация растворенной соли будет возрастать и раньше всего кристаллики начнут выпадать там, где избыточная концентрация соли будет наибольшей. Это будет в самой тонкой части капли, т. е. вдоль ее периметра. Именно вдоль периметра кристаллики и выпадут. Жидкость капли, смачивая выпадающие кристаллики, как бы приклеивается к ним. Поэтому капля, теряя жидкость, должна менять свою форму, становиться более плоской: ведь ее объем уменьшается, а периметр остается неизменным.

В начале процесса высыхания форма капли, лежащей на стекле, была равновесной. Это означает, что из всех возможных форм осуществилась та, при которой энергия поверхности, граничащей с воздухом и стеклом, наименьшая при данном объеме капли. Но вот обстоятельства вынуждают испаряющуюся каплю изменить свою наиболее выгодную форму и принять форму менее выгодную. Лук, стянутый тетивой, напрягается, если тетиву натягивать, придавать ей форму, против которой и тетива, и лук "возражают". Нечто подобное происходит и с поверхностью высыхающей капли. Чем больше испаряется влаги, тем больше искажается форма капли, и на каком-то этапе капля оторвется от кристалликов на периметре и примет равновесную форму. А затем - все сначала: новые кристаллики вдоль периметра, изменение формы капли, отрыв капли от кристалликов и так далее, пока капля не испарится, оставив после себя пятно, состоящее из концентрических колец кристалликов соли. Именно такие пятна и остаются на столе в фотокомнате, где работал неаккуратный фотограф.

Невысыхающие капли

Правильнее было бы сказать так: сохнущие, но не высылающие капли. Никогда не высыхающие! С ними мы столкнулись случайно, изучая закономерности образования концентрических колец при высыхании капель раствора сульфита, и при этом, естественно, заинтересовались, как изменяется рисунок пятна с изменением концентрации раствора. На стекле помещались капли раствора сульфита в воде различных концентраций, стекло подогревалось, капли высыхали, и на их месте оставались пятна. В этих опытах обнаружилось много любопытных закономерностей, о некоторых из них рассказано в предыдущем очерке о неаккуратном фотографе. Одно из любопытных наблюдений, сделанных в этих опытах, заключалось в том, что некоторые капли не образовывали пятен, а просто оставались на стекле. Вначале их размер немного уменьшался, а затем они оставались неизменными. Стеклышко, на котором они находились, подогревали, а капли продолжали оставаться неизменными. Это происходило с каплями растворов сульфита в воде, в которых сульфита было много - более 10%. Оказалось, что неиспаряющиеся капли покрыты панцирем из кристаллического сульфита. Под панцирем есть жидкость, но испаряться она не может: мешает панцирь.

Убедиться в том, что под панцирем жидкость, легко. На многих каплях панцирь тонкий и прозрачный, и, если немного потрясти стеклышко с каплей, можно увидеть, как под панцирем колышется вода. А можно панцирь проколоть иголкой или раздавить его, и из-под панциря вытечет жидкость.

Естествен вопрос: как и почему высыхающая капля раствора покрывается панцирем? Происходит следующее. Испарение воды с поверхности капли приводит к тому, что в приповерхностном слое повышается концентрация растворенного вещества. Вначале кристаллики из пересыщенного раствора выпадут в самом тонком участке капли, вдоль ее периметра. Далее. Если бы избыточное вещество из приповерхностного слоя уходило в объем капли и неравномерность в распределении этого вещества сглаживалась, все могло бы происходить, например, так, как это описано в очерке о пятнах на столе в фотокомнате: капля исчезла бы, оставив после себя на стекле пятно, состоящее из совокупности колец. А вот когда концентрация растворенного вещества велика и испарение происходит быстро, избыточное вещество из приповерхностного слоя присоединяется к тем кристалликам, которые образовались вдоль периметра капли. Это приводит к росту кристаллов в область, где растворенное вещество в избытке, т. е. в приповерхностный слой, и на капле появляется кристаллический панцирь. В этом случае вещество, растворенное в капле, не остается в форме осадка на стекле, а образует своеобразный осадок - панцирь на поверхности капли.

Капля, или, точнее, жидкость под панцирем, может от панциря избавиться. Если температура окружающего пространства повысится, панцирь растворится в жидкости под ним и образуется свободная капля раствора. В ней, однако, концентрация соли будет больше, чем в исходной капле: перед образованием панциря часть жидкости испарилась. При этой, более высокой, температуре все может повториться сначала: жидкость будет испаряться, и на капле образуется панцирь. На этот раз он должен быть потолще, а жидкости под ним меньше, чем в капле под панцирем до поднятия температуры. А быть может, и вообще жидкости не будет, если она успеет испариться до образования панциря. В этом случае, разумеется, панцирь - уже не панцирь, а просто осадок на стекле. Замена панциря осадком при какой-то температуре обязательно произойдет, и, если наша цель - получить каплю с панцирем, надо высушивать ее при температуре более низкой, чем та, при которой на месте капли остается просто пятно.

А если каплю, покрытую панцирем, охлаждать, будет происходить иное: растворенное вещество из жидкости, оставшейся под панцирем, будет осаждаться на панцире. Панцирь утолстится, и жидкость под ним будет всегда. Можно добиться, чтобы под слоем кристаллического покрытия осталась чистейшая дистиллированная вода. Капля чистой воды, защитившаяся от высыхания!

С каплей, покрытой панцирем, никакие загадки не связаны: все ясно, объяснимо, предсказуемо. И все же, когда встречаешься с каплей, которая, как бы защищая себя от исчезновения, покрывается панцирем, невольно задумываешься над тем, как много неожиданных следствий могут обусловить абсолютно ясные причины.

Капля масла на воде

Капля масла на поверхности воды. Что с ней произойдет? Ну, конечно, будет растекаться. Конечно, растечется и практически перестанет быть видимой. И почему растечется, понятно. Потому что понизится поверхностная энергия. И все же, несмотря на кажущуюся ясность явления, о нем стоит поговорить, поскольку на этом явлении основан один из выдающихся экспериментов атомной физики. Растекающаяся по воде капля масла помогла определить размер молекулы.

Когда лорд Рэлей (в начале нашего века) ставил опыты по растеканию капель масла на поверхности воды, о возможности непосредственно определить размер молекулы естествоиспытатели если и мечтали, то очень робко: строили сложные последовательности косвенных соображений и умозаключений, которые должны были привести к оценке этого размера. Скованные традиционными приемами экспериментирования, мыслящие прямолинейно, довольствовались умозаключениями, а непредубежденный Рэлей поставил прямой опыт, простой и убедительный. Он рассуждал так (или примерно так): каждая молекула капли масла, расположенной на воде, будет пытаться коснуться воды. Молекуле масла это необходимо, так как один ее конец к воде относится безразлично, а другой, с иным химическим строением, имеет большое сродство к воде и поэтому обязательно постарается к ней прикоснуться. Капля как бы распадется на отдельные молекулы, которые, одним концом уткнувшись в воду, расположатся на ее поверхности частоколом. У молекул капли масла сродство друг к другу слабее, чем сродство к воде активного конца молекулы.

Если знать площадь поверхности воды S (это определить очень просто) и быть уверенным в том, что капля масла определенного объема V (и его определить просто) полностью "заселила" поверхность воды своими молекулами, которые расположены в один слой, то толщину этого слоя, т. е. длину молекул l, можно определить по простейшей формуле l = V/S,

В последовательности этих рассуждений есть одно тонкое место. Как убедиться в том, что молекулы капли масла закрыли собой всю поверхность воды, нигде не оставив пятачка водной поверхности и нигде не образовав слоя более толстого, чем одномолекулярный? Лорд Рэлей сумел убедиться в этом удивительно простым способом. Зная, что частички камфоры на поверхности воды совершают активное, беспорядочное движение, а на поверхности масла спокойны, он поставил следующий опыт: в таз с водой капал капли оливкового масла разной массы, ждал пока они растекутся, а затем бросал туда немного пыльцы камфоры. Пыльца переставала "плясать", когда масса капли достигала определенной величины m^* - необходимой и достаточной, чтобы одномолекулярным слоем закрыть всю поверхность воды. Если масса капли превышает эту величину, на поверхности воды образуются масляные пятачки, как на жирном бульоне.

Рис. 18. Схема растекания капли масла на воде с образованием одномолекулярного слоя

То, что происходит при растекании капли масла по поверхности воды, удобно пояснить, воспользовавшись аналогией. Табун коней пьет воду из длинного желоба. Если число коней таково, что они умещаются вдоль желоба, у воды образуется один ряд (слой) коней, и каждый из них стоит перпендикулярно желобу. Если коней в табуне больше, часть их будет стоять в стороне, представляя собой аналог жирных пятачков на бульоне. (Эту аналогию придумал американский физик Эрик Роджерс. Только у него не кони у желоба с водой, а свиньи у кормушки; мне же кони нравятся больше, чем свиньи.)

Рэлей заполнял водой таз радиусом R = 41 см, т. е. площадью S = 5.27•10³ см². В его опытах с каплями оливкового масла величина m^* = 8•10^-4 г, т. е. объем капли V = m^*/r = 8,88•10^-4 см³, где r = 0,9 г/см³ -  удельный вес масла. Теперь легко определить длину молекулы оливкового масла: l = m^*/prR² = 1,7•10^-7 см. На расстоянии 1 см можно расположить цепочкой 6 млн. таких молекул.

Каждый физик-экспериментатор, думая об опыте Рэлея, должен испытывать чувство зависти.

Разумеется, белой.
 

---