Глава 4.

УПРУГАЯ ЭНЕРГИЯ И СОВРЕМЕННАЯ МЕХАНИКА РАЗРУШЕНИЯ, 
с отступлениями о луках, катапультах и кенгуру

 

Человек несмысленный не знает, и невежда не разумеет того.

Псалом 91

Как было сказано в предыдущей главе, значительным достижением математиков XIX в. было создание методов расчета распределения напряжений для большинства типов конструкций, хотя эти методы носили академический характер. Но многие инженеры-практики не доверяли такого рода расчетам еще задолго до того, как Инглис посеял сомнения в их справедливости. Используя методы теории упругости, Инглис показал, что даже крошечные непредвиденные дефекты или нерегулярности, которые могут появиться в, казалось бы, абсолютно безопасной конструкции, приводят к росту локальных напряжений до величин, превышающих принятый предел прочности материала, что сулит преждевременное разрушение конструкции.

В самом деле, используя формулу Инглиса, можно с легкостью подсчитать, что для фермы железнодорожного моста в устье реки Форт, сделанной из не очень твердой стали, достаточно обычной булавочной царапины, чтобы она развалилась и мост рухнул в море. Однако не часто приходится слышать, что мосты разваливаются от булавочных царапин, в то время как на практике все конструкции, включая суда и самолеты, сплошь покрыты зазубринами, трещинами и отверстиями, вызывающими концентрации напряжений, но представляющими опасность только в исключительных случаях. Как правило, они не причиняют никакого вреда. Однако время от времени конструкции все же ломаются, и каждый случай может грозить серьезной аварией.

Когда лет 50-60 назад смысл расчетов Инглиса начал доходить до инженеров, они были склонны "закрыть" всю проблему, уповая на пластичность обычно используемых металлов. Форма кривой деформирования для наиболее пластичных металлов близка к изображенной на рис. 21, и было принято считать, что перенапряженный металл у кончика трещины пластически течет, освобождаясь тем самым от серьезных перенапряжений. Таким образом, острый кончик трещины как бы сглаживается и его можно рассматривать как "закругленный", так что концентрация напряжений уменьшается и безопасность восстанавливается.

Подобно многим другим правдоподобным доводам, такое объяснение лишь отчасти соответствует истинному положению вещей и далеко не исчерпывает всей проблемы в целом. В большинстве случаев концентрация напряжений за счет пластичности металла полностью не снимается и локальное напряжение в действительности очень часто значительно превосходит общепринятое "разрушающее напряжение" материала, найденное в лабораторных опытах на малых образцах и приведенное в опубликованных таблицах и справочниках.

Однако идеи, вызывающие замешательство и подрывающие веру в общепринятые методы расчета на прочность, долгое время не пользовались поддержкой. В мои студенческие годы имя Инглиса почти не упоминалось, а эти сомнения и трудности инженеры дипломатично обходили. С точки зрения прагматиков такую позицию можно отчасти оправдать, поскольку при разумно выбранном коэффициенте запаса для многих обычных конструкций расчетам на прочность, основанным на традиционном подходе, не учитывающем концентрацию напряжений, как правило, можно доверять. И сегодня это лежит в основе большинства норм и правил безопасности, устанавливаемых правительственными организациями и страховыми компаниями.

Однако даже у прекрасных инженеров время от времени случались промашки. Так, в 1928 г. на пассажирском пароходе компании Уайт Стар "Маджестик" водоизмещением 56551 т, в то время самом большом и красивом корабле в мире, сделали дополнительный пассажирский лифт. При этом в нескольких силовых палубных перекрытиях прорубили сквозные прямоугольные отверстия с нескругленными углами. Где-то между Нью-Йорком и Саутгемптоном, когда на борту было около 3 тыс. человек, у одного из этих отверстий образовалась трещина, которая дошла до поручней, опустилась по борту корабля на несколько метров и, к счастью, застопорилась, наткнувшись на иллюминатор. Лайнер благополучно достиг Саутгемптона, и ни пассажиры, ни пресса ничего об этом не узнали. По исключительному стечению обстоятельств примерно то же самое почти одновременно произошло со вторым по величине кораблем мира, американским трансатлантическим пассажирским лайнером "Левиафан". И в этом случае судно благополучно достигло порта и огласки удалось избежать. Если бы трещины распространились немного дальше, эти пароходы развалились бы пополам в открытом море и могли бы погибнуть тысячи людей.

В послевоенное время потрясающие мир катастрофы с кораблями, мостами, буровыми вышками стали обычным явлением, и количество их год от года возрастает. Ценой гибели множества людей и огромных материальных потерь достигнуто, наконец, понимание недостаточности классической теории упругости для предсказания прочности особенно больших конструкций, хотя, конечно, созданная Гуком, Юнгом, Навье и их последователями наука исключительно важна и не может быть речи о том, что она не нужна или устарела.

Энергетический подход к расчетам конструкций на прочность
 

Шумели небо и вода, Но сам ты прятался всегда. Ты звал меня, касался щек, Но я поймать тебя не мог. Р. Л. Стивенсон. "Детский цветник стихов" Перевод Игн. Ивановского

До самого недавнего времени в теории упругости и связанных с нею исследованиях пользовались терминами напряжение, деформация, прочность и жесткость, то есть, по существу, можно сказать, понятиями сил и перемещений. До сих пор и мы в этой книге вели рассуждения только в рамках этих понятий, и, мне кажется, многие считают такой подход наиболее простым. Однако, чем больше наблюдаешь закономерности природы и размышляешь о технике, тем больше склоняешься к энергетической концепции. Такой подход позволяет объяснить очень многое, и он лежит в основе современных моделей прочности материалов и поведения конструкций, то есть в основе довольно модной науки - механики разрушения. С его помощью проясняются многие моменты не только из области прочности инженерных конструкций, но и из совсем других наук, даже таких, как история и биология.

Досадно, что в сознании многих само представление об энергии было основательно запутано значением этого слова, употребляемым в обиходе. Подобно слову "напряжение", слово "энергия" часто используется для характеристики человеческого поведения. Такое словоупотребление имеет весьма слабую связь с обозначением реальной и точно определенной физической величины, к рассмотрению которой мы сейчас переходим.

В науке под энергией понимается способность совершать работу. Именно с такой величиной, имеющей размерность силы, умноженной на расстояние, мы и будем иметь дело. Так, поднимая груз весом в 5 кг на высоту 2 м, нужно совершить работу в 10 кгм, в результате в грузе будет запасено 10 кгм потенциальной энергии. До поры до времени эта энергия "законсервирована" в грузе, но, позволив грузу опуститься, ее можно вновь освободить. Высвобождаемый при этом запас энергии (10 кгм) может быть на что-то израсходован, например на работу часового механизма или на дробление льда на пруду.

Существует множество видов энергии - потенциальная, тепловая, химическая, электрическая и т. д. В нашем материальном мире всякое событие сопровождается превращением одной формы энергии в другую. Подобные превращения происходят в соответствии с некоторыми строго определенными правилами, главное из которых: "нельзя получить что-либо из ничего". Энергия не может быть создана или уничтожена, так что общее количество энергии, имевшееся до какого-либо физического процесса, остается тем же и после него. Этот принцип называется законом сохранения энергии.

Таким образом, энергию можно рассматривать как "универсальную валюту" науки, и часто наблюдения за ее превращениями, особенно при использовании соответствующей методики учета, могут быть очень информативными. Но для этого необходимы правильно выбранные единицы, а, как этого и следовало ожидать, в традиционных единицах энергии господствует неразбериха. Инженеры-механики склонны использовать килограммометры, физики привержены к эргам и электрон-вольтам, химикам и диетологам нравится использовать калории, счета за газ приходят в термах (1 терм = 105,5 МДж. - Перев.), а за электричество - в киловатт-часах. Все эти единицы, конечно, взаимообратимы и их можно переводить друг в друга, но в настоящее время лучше пользоваться единицей энергии системы СИ - джоулем. Джоуль определяет работу, производимую силой в 1 ньютон на пути в 1 метр *.

* Дж = 10⁷эрг = 0,239 калории. 1 Дж - энергия среднего яблока, упавшего со стола обычной высоты.

Несмотря на то что энергию можно измерять достаточно точными методами, для многих осмыслить это понятие оказывается более трудным, чем, например, понятия силы и расстояния. Энергию, как и ветер из стихотворения Стивенсона, мы можем воспринимать лишь через ее проявления. Возможно, именно поэтому понятие энергии вошло в науку довольно поздно - в современной форме его ввел Томас Юнг в 1807 г. Сохранение энергии стало общепризнанным законом только в самом конце XIX в., и только после Эйнштейна и атомной бомбы огромная важность энергии как объединяющей концепции и как фундаментальной реальности была оценена всеми в достаточной степени.

Существует много способов - химических, тепловых, электрических и т. п. - накопления и сохранения энергии до тех пор, пока она не понадобится. Если мы собираемся использовать для этого механические средства, то можно применить метод, о котором уже говорилось, - использовать потенциальную энергию поднятого груза. Однако это довольно примитивный способ, и на практике как в инженерном деле, так и в биологии значительно чаще используется энергия деформации, или упругая энергия.

Очевидно, что энергию можно запасти в сжатой пружине, однако, как заметил Гук, поведение пружин является частным случаем упругости твердого тела при воздействии нагрузки. Таким образом, любое упругое вещество, находящееся в напряженном состоянии, содержит упругую энергию независимо от того, идет ли речь о растягивающем или сжимающем напряжении.

Если выполняется закон Гука, напряжение в материале нарастает от нуля до максимума в момент, когда материал растянут до предела. Упругая энергия на единицу объема представлена заштрихованной площадью под кривой деформирования (рис. 13). Эта площадь составляет

1/2 х напряжение х деформация = 1/2 se.

Рис. 13. Упругая энергия = площадь под кривой деформирования = 1/2 se.

Автомобили, лыжники и кенгуру

Все мы хорошо представляем себе упругую энергию автомобильных рессор. В машине без рессор должны были бы происходить бурные превращения потенциальной энергии в кинетическую (энергию движения) и обратно всякий раз, когда колесо проходит ухаб или рытвину. Эти превращения энергии неприятны как пассажирам, так и экипажу. Давным-давно, однако, какой-то гений изобрел рессоры, которые служат резервуаром энергии, позволяющим временно запасать изменения потенциальной энергии в виде упругой энергии, что смягчает удары при езде и предохраняет и экипаж, и пассажиров от "угрозы разрушения". Впоследствии инженеры затратили много времени и усилий, совершенствуя подвеску автомобиля и проявляя незаурядную изобретательность. Но автомобили ходят по дорогам, назначение которых - обеспечить гладкую поверхность для движения. Так что подвеска автомобиля служит только для того, чтобы нейтрализовать небольшие остаточные неровности. Задача же сконструировать подвеску для автомобиля, предназначенного для движения с большой скоростью по пересеченной местности, была бы исключительно трудной. Чтобы справляться с возникающими при таком движении ситуациями и в достаточных количествах запасать энергию, рессоры должны были бы быть очень большими и тяжелыми и сами по себе содержать столько "неподрессоренного веса", что вряд ли вся конструкция оказалась бы практичной.

Рассмотрим теперь ситуацию, возникающую при движении лыжника. Несмотря на снежное покрытие, лыжня обычно значительно более бугриста, чем любая нормальная дорога. Даже если бы можно было создать вдоль лыжни эффективное покрытие, например, из песка, предотвращающее пробуксовку, так что автомобиль мог бы двигаться по нему без скольжения, любая попытка прокатиться по лыжне на машине со скоростью несущегося с горы лыжника (например, 80 км/ч) кончилась бы печально, поскольку подвеска не смогла бы смягчить тряску. Но как раз с этой задачей и должно справляться тело лыжника. На самом деле значительную часть соответствующей энергии, по-видимому, принимают на себя сухожилия ног лыжника, вес которых не превышает и полукилограмма *. Таким образом, если мы собираемся носиться на лыжах без опаски или совершать другие атлетические подвиги, наши сухожилия должны обладать способностью принимать и возвращать очень большие количества энергии. Отчасти для этого они и предназначены.

* Поскольку при занятиях горными лыжами расход кислорода в организме больше, чем при любых других видах человеческой деятельности, много энергии должны принимать на себя и мускулы. Однако большая часть поглощаемой мускулами энергии необратима, так что сухожилия в качестве аккумулятора упругой энергии незаменимы.

Приближенные значения способности различных материалов запасать упругую энергию приведены в табл. 3. Некоторые сравнения биологических материалов с металлами, возможно, вызовут удивление инженеров, а разница величин, характерных для сухожилий и стали, проливает свет на соответствующие качества лыжников и живых существ вообще. У сухожилия способность запасать энергию, отнесенная к единице массы, примерно в 20 раз больше, чем у современных пружинных сталей. Хотя лыжники в качестве "устройств" для накопления упругой энергии эффективнее большинства механизмов, даже тренированный атлет не может конкурировать с оленем, белкой или обезьяной. Интересно было бы выяснить, какой по сравнению с человеком процент веса этих животных приходится на сухожилия.

Вещество	Рабочая деформация, %	Рабочее напряжение, МН/м2	Запасаемая упругая энергия 106 Дж/м3	Плотность, кг/м3	Запасаемая энергия, Дж/кг
Железо древних Современная пружинная сталь Бронза Древесина тиса Сухожилие Роговая ткань Резина	0,03 0,3 0,3 0,9 8,0 4,0 300	70 700 400 120 70 90 7	0,01 1,0 0,6 0,5 2,8 1,8 10,0	7800 7800 8700 600 1100 1200 1200	1,3 130 70 900 2500 1500 8000

Животные, подобные кенгуру, передвигаются прыжками. При каждом приземлении их сухожилия должны запасать упругую энергию и, по свидетельству одного моего знакомого, австралийского ученого, предельная упругая энергия для них чрезвычайно высока, хотя точных цифр, к сожалению, я не могу привести. Мне кажется, что если бы понадобилось возродить ходули на пружинах, то в первую очередь следовало бы рассмотреть возможность использования в них вместо пружин сухожилий кенгуру или других животных. Шасси легких самолетов, рассчитанных на посадку на неровной местности, часто крепятся к корпусу с помощью резиновых подвесок, способность которых запасать упругую энергию много больше, чем у стальных рессор и даже сухожилий, но срок службы у них гораздо меньше.

Упругая энергия, которая играет столь большую роль в подвесках автомобилей, самолетов и, выражаясь фигурально, животных, влияет на прочность и разрушение в;ех видов конструкций. Однако, прежде чем мы перейдем к такому предмету, как механика разрушения, возможно, стоит поговорить еще об одном применении упругой энергии - ее роли в работе такого оружия, как луки и катапульты.
 

Луки

...Смотрите, вот лук Одиссеев; Тот, кто согнет, навязав тетиву, Одиссеев могучий Лук, чья стрела пролетит через все (их не тронув) двенадцать Колец, я с тем удалюся из этого милого дома, Дома семейного, светлого, многобогатого, где я Счастье нашла, о котором и сонная буду крушиться. Гомер. "Одиссея". Песнь XXI Перевод В.А. Жуковского

Лук - одно из наиболее эффективных приспособлений, способных аккумулировать мускульную энергию человека. Английские большие луки, которые принесли победу при Креси (1346) и Азенкуре (1415) *, почти всегда делались из тиса.

* Речь идет о битвах во время Столетней войны. - Прим. перев.

Сегодня тисовая древесина не имеет большого промышленного значения, а потому до недавнего времени ей не уделяли внимания в научных исследованиях. Однако мой коллега, д-р Г. Блют, занимающийся изучением оружия прошлых веков, установил, что микроскопическое строение древесины тиса (Taxus baccata) заметно отличается от строения других пород, она представляется нам наиболее способной запасать упругую энергию. Поэтому тис, вероятно, особенно подходит для изготовления луков.

Вопреки распространенному мнению английские большие луки, как правило, делались не из английского тисового дерева, растущего на церковных кладбищах и в других местах, а из испанского тиса, и по существовавшему в то время закону каждая ввозимая партия испанского вина должна была сопровождаться партией испанских заготовок для луков.

Как известно, тисовое дерево хорошо произрастает не только в Испании, но и по всему району Средиземноморья. Так, буйные заросли тиса покрывают сегодня руины Помпеев. Однако свидетельств об использовании тисовых луков в Испании и странах Средиземноморья как в древности, так и в Средние века почти не встречается. Они были приняты почти исключительно в Англии, Франции и отчасти в Германии и Нидерландах. Опустошения, производимые англичанами, обычно доходили до районов Бургундии и вряд ли когда-либо распространялись южнее Альп или Пиренеев.

На первый взгляд это может вызвать удивление, но Г. Блют указывает, что у тиса механические свойства древесины ухудшаются с ростом температуры быстрее, чем у древесины других пород, а потому тисовый лук не может надежно служить при температуре выше 35°С. Таким образом, его применение в качестве оружия ограничено холодным климатом, и он непригоден в условиях средиземноморского лета. Поэтому, хотя в странах Средиземноморья тисовое дерево применялось для изготовления стрел, оно редко использовалось там для изготовления луков.

Этим объясняется тот факт, что в этих странах получила распространение конструкция так называемого композиционного лука. Такой лук имел деревянную сердцевину, толщина которой составляла около половины толщины лука и которая подвергалась лишь небольшим напряжениям. К этой сердцевине приклеивались внешний слой из высушенных сухожилий, подвергающийся растяжению, и сделанный из рога внутренний слой, подвергающися сжатию. Оба этих материала превосходят тис способностью запасать упругую энергию. Лучше тиса они сохраняли и свои механические свойства в жаркую погоду - ведь температура животного около 37°С. На практике высушенные сухожилия сохраняют свои свойства до температуры 55°С, но теряют их в сырую погоду.

Комбинированные луки использовались в Турции и ряде других мест до сравнительно недавнего времени. Лорд Абердин писал в 1813 г. по пути на Венский конгресс об использовании против отступающих по Восточной Европе наполеоновских армий татарских войсковых частей, вооруженных, по-видимому, подобными луками. Очевидно, комбинированные луки были во многих отношениях лучше английского большого лука, но последний был дешевле и проще в изготовлении. Луки древних греков тоже были комбинированными, так что сделать лук Одиссея или Филоктета * требовало незаурядного мастерства.

* Согласно легенде, Филоктет получил свой лук от умирающего Геракла. - Прим. перев.

Упоминание о луке Одиссея заставляет нас вспомнить о покинутой Пенелопе, которая устроила состязание для претендентов на ее руку, предложив им натянуть тетиву одиссеева лука. Как известно, это оказалось не под силу ни одному из них, даже изобретательному Эвримаху. "А потом лук взял Эвримах, и он нагрел его со всех сторон в пламени огня, но все равно он не смог натянуть его, и тяжкий стон вырвался из его груди". Но в конце концов в чем смысл всех усилий и почему поклонники Пенелопы, Одиссей да и вообще лучники не использовали просто более длинную тетиву?

На это имеются весьма веские основания. Возможности передачи упругой энергии луку от человека ограничены характеристиками человеческого тела. На практике стрелу удается оттянуть примерно на 0,6 м, и даже сильный человек не может натягивать тетиву с силой больше 350 Н. Соответствующая энергия мышц составляет примерно 0,6 м х 350 Н, то есть около 210 Дж. Это максимум того, чем мы располагаем, и мы хотим как можно большую часть этой энергии запасти в луке в виде упругой энергии.

Если предположить, что первоначально лук не натянут и его тетива почти провисает, то в момент, когда стрелок начинает оттягивать стрелу, прикладываемая им сила почти равна нулю. Она достигнет своего наибольшего возможного значения только тогда, когда тетива максимально растянется. Это демонстрирует график на рис. 14. Энергия, переданная луку, будет в таком случае выражаться площадью треугольника и не может быть больше половины той энергии, которую мы могли бы затратить, то есть не может превышать 105 Дж.

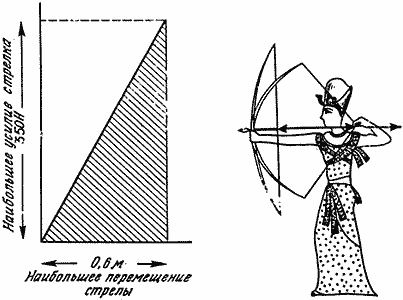
Рис. 14. Упругая энергия лука =  1/2 x 0,6 x 350 = 105 Дж.
Эта диаграмма, как и кривая на рис. 16, конечно, носит схематический характер.
Вообще говоря, зависимость между силой и перемещением стрелы нелинейна,
но это не меняет сути дела.

Энергия, запасаемая в английском большом луке, на практике немного меньше этой величины. Однако Гомер особо отмечает, что лук Одиссея был palintonos, что означает "изогнутый, натянутый назад". Другими словами, лук первоначально был изогнут в направлении, противоположном рабочему, так что для того, чтобы натянуть на него тетиву, приходилось прикладывать большую силу (рис. 15).
 

Рис. 15. Натягивание тетивы на греческий лук (роспись на вазе).

В этом случае, стреляя, лучник начинает натягивать тетиву не от нулевых значений напряжения и деформации, так что, подобрав соответствующую конструкцию лука, можно добиться того, чтобы график зависимости силы от растяжения выглядел примерно так, как показано на рис. 16 *.

* Рисунки 14 и 16, конечно, схематичны. График зависимости силы от натяжения в общем случае не является прямой линией, но использованный здесь принцип расчета остается применимым.

Площадь ABCD под таким графиком теперь составляет значительно большую долю от располагаемой энергии; эта доля, вероятно, достигает 80%. Поэтому в таком луке запас энергии может составить около 170 Дж. Вполне очевидно, что это дает большие преимущества стрелку, не говоря уже о выгоде, которую имела Пенелопа.

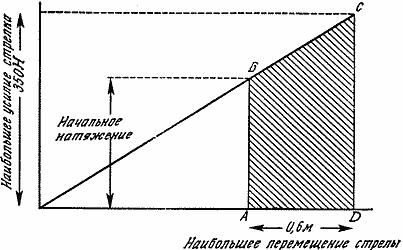
Рис. 16. Почему луки бывают "изогнутыми назад" (палинтонос).
Энергия, запасаемая в луке, теперь дается площадью АВС,
что соответствует примерно 170 Дж.

В действительности тетива любого лука натянута в большей или меньшей степени еще до того, как ее начинают растягивать, и, чтобы ее надеть, требуется определенное усилие. Но поскольку английские большие луки - это луки "без хитростей", которые делались из заготовок, отколотых от бревен строевого леса, а потому почти прямых, влияние этого обстоятельства в данном случае незначительно. Гораздо проще придать наилучшую исходную форму комбинированным лукам, именно они обычно имеют характерные очертания "лука Купидона" (рис. 17).

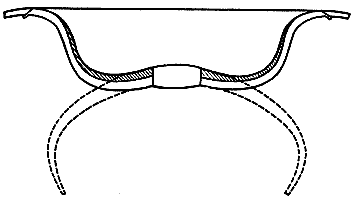
Рис. 17. Комбинированный лук в ненатянутом и натянутом состояниях.

Поскольку предельная упругая энергия таких материалов, как роговая ткань и сухожилие, превышает предельно упругую энергию тиса, комбинированный лук можно сделать более коротким и легким, чем деревянный. Именно поэтому размеры английского деревянного лука соответствовали росту человека, а сам он получил название большого лука. Комбинированный лук можно сделать гораздо меньшим, чтобы им могли пользоваться всадники, как это и было у парфян и татар. Парфянский лук был настолько удобен, что позволял всаднику стрелять назад в преследователей; очевидно, отсюда и пошло выражение "парфянская стрела".
 

Катапульты

Величайший период классической Эллады завершился с падением Афин в 404 г. до н.э., демократический строй в Греции постепенно в течение столетия пришел в упадок и был вытеснен тиранией и военной монархией. Менялись методы ведения войны как на суше, так и на море, и возникла потребность в более современном механизированном оружии. Более того, властители постепенно богатеющих государств располагали средствами для оплаты военных расходов.

Начало было положено в греческой Сицилии. Стратег-автократ Дионисий I был, по-видимому, выдающимся человеком, сумевшим от простого военачальника возвыситься до тирана Сиракуз. За годы его правления, продолжавшегося с 405 до 367 г. до н.э., Сицилийская держава стала крупной экономической и политической силой не только в Западном Средиземноморье, но и во всем эллинском мире. При созданном Дионисием военном ведомстве была основана, вероятно, первая в истории государственная лаборатория, проводившая исследования в области вооружения. Он пригласил для этого учреждения лучших математиков и мастеров со всего греческого мира.

Естественной отправной точкой для специалистов, отобранных Дионисием, явился традиционный комбинированный ручной лук. Установив такой лук на какую-либо опору и оттягивая тетиву посредством механического привода или рычагов, можно сделать его значительно жестче, что позволит в несколько раз увеличить запасаемую и сообщаемую снаряду энергию. Так, очевидно, подошли к самострелу, снаряды которого способны были пробивать любые доспехи *. Претерпев лишь небольшие конструктивные изменения, самострелы не вышли из употребления и до настоящего времени. Говорят, что они применяются сейчас в Ольстере. Любопытно, однако, что как оружие самострелы никогда не играли сколько-нибудь решающей военной роли.

* Однако скорость стрельбы из самострела не сравнима со скоростью стрельбы из ручного лука. Так, с помощью английских больших луков можно пускать до 14 стрел в минуту и при массовом использовании этого оружия получать целое облако стрел. Подсчитано, что при Азенкуре из луков было пущено около 6 млн. стрел.

Но самострел, в сущности, явился пехотным оружием, направленным против человека, так как с его помощью нельзя было наносить серьезные повреждения корпусам кораблей или фортификационным сооружениям. И хотя сиракузцы, увеличив размеры самострела и установив его на основание орудийного типа, создали катапульту, эта линия развития оружия не получила продолжения. По-видимому, определенные технические ограничения не позволяют сделать катапульту типа лука достаточно мощной, чтобы пробивать бреши в крепостной кладке *.

* Недавние находки на Кипре позволяют предположить существование военных катапульт в V в. до н.э. Но и в этом случае подход Дионисия был, по-видимому, первым "научным" подходом к проблеме.

Следующим шагом были поэтому отказ от конструкции типа лука и использование для накопления упругой энергии скрученных связок сухожилий *, очень похожих на резинокордные связки, используемые для привода авиационных моделей.

* Они, вероятно, ведут свое происхождение от "испанского ворота", использовавшегося на кораблях древних (см. гл. 10).

Когда связка таких резиновых лент или сухожилий закручивается, материал связки подвергается растяжению, запасая упругую энергию.

Известны самые разные способы использования связок сухожилий в военной технике, однако самой лучшей конструкцией следует признать древнегреческий палинтонон, который у римлян получил название баллисты. Это исключительное по смертоносности орудие имело по две вертикальные связки сухожилий, каждая из которых закручивалась с помощью жесткой рукоятки или рычага, напоминающего рукоять ворота (рис. 18).

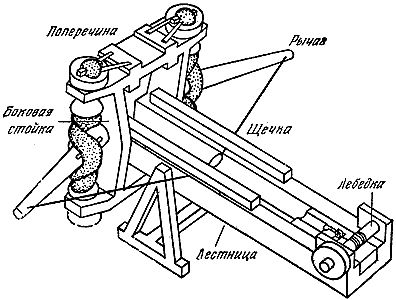
Рис. 18. Возможно, так выглядела древнегреческая катапульта.

Концы этих рычагов были соединены между собой толстой тетивой, а все устройство работало подобно луку. Свое название оно получило оттого, что в положении с ненатянутой тетивой оба ее рычага направлены вперед, как у комбинированного лука без тетивы. Тетива в катапульте натягивается посредством мощной лебедки подобно натягиванию тетивы лука. Снаряд (чаще всего каменное ядро) после выстрела двигался вперед по направляющим, которые одновременно служили и станиной лебедки. Лебедка могла развивать усилие, достигавшее ста тонн.

Римляне скопировали греческую катапульту, и Витрувий, служивший в войсках Юлия Цезаря, оставил нам руководство по баллистам, которое представляет немалый интерес. Размеры этих машин позволяли метать снаряды весом от 2 до 150 кг. Радиус их действия был примерно 400 м (для всех размеров). Средняя крепостная баллиста римлян, по-видимому, стреляла ядрами весом в 40 кг.

При последней, драматической осаде Карфагена в 146 г. до н. э. римляне, сделав насыпь в неглубокой лагуне, к которой выходила городская стена, установили на ней катапульты и стали из них крушить укрепления. Археологи откопали на этом месте около 6 тыс. каменных ядер весом по 40 кг каждое.

Хотя Юлий Цезарь и Клавдий использовали корабли с катапультами для нападения на британские берега, эти метательные машины, по-видимому, никогда не были грозным оружием в сражениях на море. Скорострельность такой баллисты, которая могла бы потопить корабль попаданием одного снаряда, была слишком мала и почти не позволяла поразить движущееся судно.

Иногда с помощью катапульты метали горящие снаряды, но на полных народа незатейливых кораблях того времени пожар обычно нетрудно было потушить. В 184 г. до н. э. один изобретательный флотоводец выиграл морское сражение, обрушив на головы противника глиняные горшки с ядовитыми змеями, однако его примеру, кажется, никто не последовал. В целом катапульты на море не имели успеха.

Однако палинтонон, или баллиста, был весьма эффективным средством ведения сухопутной войны. Его изготовление и эксплуатация были связаны с известными трудностями, так что обслуживающий катапульты персонал должен был быть весьма сведущим в своем деле. После того как Римская империя с ее техникой отошла в прошлое, это оружие стало непрактичным и было забыто *. В Средние века применение осадных машин свелось к использованию весовой катапульты, или требюше (рис. 19).

* В Англии в период паники 1940 г., вызванной возможным вторжением немцев, было изготовлено два варианта римской баллисты для использования войсками ополчения. Это оружие предназначалось для метания зажигательных бомб в немецкие танки. Но поскольку радиус действия и одной и другой катапульты составлял лишь четверть радиуса действия их классического прототипа, можно предположить, что их создатели не удосужились внимательно прочесть даже Витрувия.

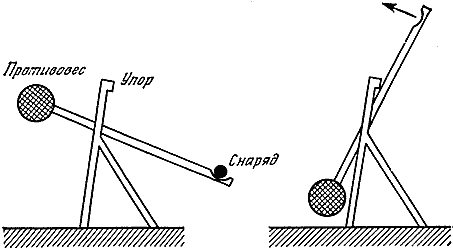
Рис. 19. Требюше, или средневековая катапульта, - самое неэффективное из метательных устройств.

В этом устройстве, похожем на маятник, использовалась потенциальная энергия поднятого груза. Даже с помощью большого требюше вряд ли можно было поднять груз более тонны (10000 Н) на высоту 3 м. Поэтому наибольшая запасаемая потенциальная энергия, вероятно, не намного превосходила 30000 Дж. Такое же количество энергии можно запасти в виде упругой энергии в 10-12 кг сухожилий. Поэтому даже большое требюше, вероятно, обладало только одной десятой энергии катапульты. К тому же, по-видимому, значительно более низкой была эффективность передачи энергии. С помощью требюше можно было в лучшем случае причинить неприятности путем забрасывания через крепостные стены больших камней; любая же попытка повредить мощную каменную кладку не имела бы успеха *.

* Подробнее о требюше см. Д. Уваров, "Требюше, или гравитационные метательные машины" - V.V.

Принцип действия лука и палинтонона как устройств для передачи энергии одинаков, и пока еще в полной мере не нашла оценки эффективность такого механизма обмена энергией. В примитивных устройствах типа требюше значительная часть запасенной энергии шла на ускорение тяжелого противовеса и рычага и в конечном итоге терялась в системе останова или тормозов, которые были неотъемлемой частью устройства. У лука или палинтонона непосредственно после спуска тетивы часть запасенной упругой энергии передается в виде кинетической энергии прямо снаряду. Однако большая часть имеющейся энергии идет на ускорение самого лука или рычагов катапульты, где она временно переходит в кинетическую энергию. Это близко к тому, что происходит в требюше, однако здесь дальнейшие события связаны с замедлением движения самого лука, а не с жестким остановом. По мере того как лук распрямляется, увеличивается натяжение тетивы, что позволяет ей действовать на снаряд с большей силой и таким образом ускорять его движение. Поэтому значительная часть кинетической энергии, запасаемой в луке или в рычагах катапульты, передается снаряду (рис. 20).

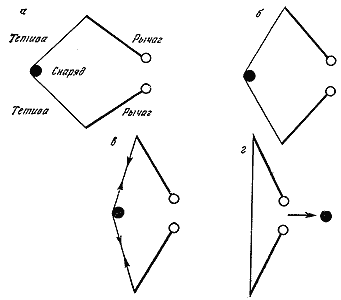
Рис. 20. Схемы, иллюстрирующие механику палинтоноса, или баллисты.

a - машина подготовлена к стрельбе, вся энергия запасена в связках сухожилий;
б - начальная стадия: тяжелые рычаги получают ускорение, отбирая при этом значительную часть энергии сухожилий;
в - заключительная стадия: тяжелые рычаги замедляют ход благодаря натяжению тетивы, таким образом их кинетическая энергия передается снаряду;
г - летящий снаряд получил энергию, первоначально запасенную в системе.

Математическое описание поведения луков и катапульт оказывается сложным, и, даже записав соответствующие уравнения движения, их нельзя решить аналитически. К счастью, однако, один из моих коллег, д-р А. Претлав, заинтересовавшись этой проблемой, применил для ее решения ЭВМ. К удивлению, оказалось, что процесс передачи энергии теоретически может иметь 100%-ную эффективность. Другими словами, практически вся упругая энергия, запасенная в устройстве, может быть превращена в кинетическую энергию снаряда. Таким образом, теряется (идет на отдачу и на соударения в системе) только малая часть энергии. В этом отношении луки и катапульты обладают преимуществами перед огнестрельным оружием.

Одно следствие из этих фактов, я думаю, хорошо известно большинству стрелков-лучников. Оно состоит в том, что при стрельбе из лука или катапульты ни в коем случае не следует пользоваться несоответствующей стрелой или снарядом. Такая попытка неминуемо закончится не только поломкой лука, но и травмой, так как в этом случае не существует безопасных каналов освобождения запасенной упругой энергии.
 

Эластичность, резильянс и ухабы на дорогах
 

Корабль взрезает равнину вод, А ветер мчит вперед, Наполнив белые паруса, Красавицы-мачты гнет. Алан Канинхэм

Когда Галилей в 1633 г. в Арцетри приступил к изучению проблем упругости, прежде всего он задался вопросами, какие факторы влияют на прочность веревки или бруска при растяжении и зависит ли прочность от длины этой веревки или бруска. Элементарные эксперименты показали, что сила или вес, требуемые для разрыва однородной веревки при ее статическом растяжении, не зависят от длины этой веревки. Такой же результат, казалось бы, подсказывает и здравый смысл, однако и по сей день можно встретить множество людей, глубоко убежденных в том, что длинный кусок веревки "крепче" короткого.

Конечно, дело здесь не в человеческой глупости, а в том, что понимать под словом "крепче". Статическая сила, или натяжение, требуемое для разрыва длинной веревки, будет, конечно, той же, что и для разрыва короткой веревки, но общее удлинение большой веревки перед ее разрывом будет значительнее и, чтобы разорвать ее, потребуется большая энергия, хотя разрушающая сила и прочность материала остаются теми же. Рассуждая немного иначе, можно сказать, что длинная веревка будет смягчать внезапные рывки, упруго растягиваясь под действием нагрузки, так что возникающие при этом перегрузки будут уменьшаться. Другими словами, она действует в значительной степени так же, как подвеска автомобиля.

Таким образом, в тех случаях, когда нагрузка действует рывками, длинная веревка может действительно оказаться "крепче" короткой. Именно поэтому экипажи XVIII в. часто подвешивались к ходовой части на длинных кожаных ремнях, которые лучше коротких могли противостоять толчкам и ударам на рытвинах тогдашних дорог. Припомните к тому же, что якорные цепи и буксирные канаты стараются делать по возможности длиннее, так как они обычно рвутся не от статической нагрузки, а от резких толчков. Тем, кто может ночью или в тумане повстречаться в море с буксируемыми большим сухими доками или буровыми вышками, полезно иметь в виду, что эти сооружения буксируются на стальном тросе длиной почти в милю. Такого рода "морские процессии", занимая огромные участки моря, вселяют ужас в случайных мореплавателей *.

* В действительности эластичность якорных цепей и буксирных канатов в значительной мере вызвана их провисанием под действием собственного веса. В этом одна из причин того, почему тяжелые тросы или цепи предпочитают значительно более легким канатам из органических материалов.

Способность запасать упругую энергию и при действии нагрузки отклоняться упругим образом без разрушения называется резильянсом и является очень ценным качеством конструкции. Резильянс можно определить как количество упругой энергии, которое можно запасти в конструкции, не причиняя ей повреждений.

Чтобы добиться высокого резильянса, конечно, не обязательно использовать очень длинную веревку или проволочный трос. Зачастую удобнее применять более короткие конструкционные элементы, такие, как спиральные пружины (в буферах железнодорожных составов) или прокладки из мягких материалов (в качестве отбойных амортизаторов судов), а также материалы с малым модулем Юнга типа пенорезины или пенопласта (для упаковки точной аппаратуры). Все они могут испытывать большие относительные удлинения и сжатия, а поэтому способны запасать большую упругую энергию на единицу объема. Природная "подвеска" лыжников и животных своим совершенством в значительной мере обязана сравнительно низким модулям упругости и большой деформативности сухожилий и других тканей.

С другой стороны, хотя низкая жесткость и высокая растяжимость способствуют поглощению энергии и поэтому уменьшают возможность разрушения конструкции при ударе, может оказаться, что обладающая этими качествами конструкция будет слишком "мягкой" для выполнения своих функций. Такого рода соображения обычно ограничивают величину резильянса, которым можно снабдить конструкцию. Самолеты, здания, инструменты, оружие должны быть достаточно жесткими, чтобы выполнять свое назначение, поэтому в конструкциях стараются достигнуть компромисса между жесткостью, прочностью и резильянсом. Здесь-то и должен приложить свое искусство конструктор.

Оптимальные условия могут изменяться не только в зависимости от типа и класса конструкции, но и при переходе в ней от одного элемента к другому. Природа и здесь имеет преимущество, поскольку в ее распоряжении находится огромный диапазон упругих свойств различных биологических тканей. Простым, но интересным примером служит обычная паутина. Она подвержена ударным нагрузкам, создаваемым попадающими в нее мухами, и энергия возникающих ударов должна быть поглощена эластичными нитями. Оказывается, что длинные радиальные нити, на которые падает основная нагрузка, втрое жестче коротких круговых нитей, назначение которых ограничивается лишь ловлей мух.

Наряду с использованием конструкционных элементов, работающих на растяжение, таких, как веревки или нити паутины, и на сжатие, таких, как буферы железнодорожных составов и отбойные амортизаторы судов, имеется еще и много других способов запасать упругую энергию и достигать высокого резильянса. Для этих целей может годиться конструкция любой формы, способная испытывать упругие отклонения. Наиболее распространенными являются устройства, запасающие энергию посредством изгиба, подобно лукам и величавым корабельным мачтам. Именно так обстоит дело в растениях, деревьях, этот принцип лежит в основе действия большинства типов автомобильных рессор. Первоклассный меч не сломается, если его изогнуть дугой, коснувшись концом рукоятки, и снова обретет свою первоначальную форму.
 

Упругая энергия как причина разрушения

...обращались назад, как неверный лук.

Псалом 77

Достаточно высокий резильянс - качество, существенное для любой конструкции, без него она не могла бы поглощать энергию ударов. С этой точки зрения, чем большим резильянсом обладает конструкция, тем лучше. Столь хитроумные устройства, как корабли викингов и американский конный кабриолет, обладали очень большой гибкостью и высоким резильянсом. Если такого рода конструкции чрезвычайно не перегружать, после снятия нагрузки они тут же приходят в первоначальное состояние. Но, естественно, больших перегрузок и они не выдержат.

Далее, чтобы разорвать материал, в нем должна возникнуть трещина. Однако, как мы вскоре увидим, чтобы такая трещина продвинулась на своем пути, необходимо затратить энергию, которую надо где-то взять. Как мы говорили выше, можно без труда сломать лук, "стреляя" из него без стрелы. При этом запасенная в луке упругая энергия не может благополучно высвободиться и перейти в кинетическую энергию стрелы, а потому часть ее идет на образование трещин в материале самого лука. Другими словами, упругая энергия лука его же и ломает. Однако сломанный лук - это только частный случай разрушения вообще.

Все упругие вещества, находящиеся под действием нагрузки, содержат большее или меньшее количество упругой энергии, и эта энергия потенциально всегда может пойти на процесс разрушения их самих. Другими словами, запасенная упругая энергия может пойти на то, чтобы покрыть энергетические затраты на распространение трещины в конструкции и, следовательно, на поломку последней. В конструкции с высоким резильянсом может содержаться большая упругая энергия; того же рода энергия, к которой прибегали древние римляне, чтобы пробить массивные стены Карфагена, в равной мере годна на то, чтобы сам себя сломал пополам громадный супертанкер.

Согласно современной точке зрения, в том случае, когда материал подвергается растягивающей нагрузке, мы не должны рассматривать его разрушение как результат непосредственного растяжения химических связей между атомами. Иначе говоря, это отнюдь не простое следствие, вызванное действием растягивающего напряжения, как можно подумать, начитавшись классических учебников *. Прямым результатом увеличения нагрузки, действующей на конструкцию, будет лишь увеличение запаса упругой энергии в материале. Ответ на вопрос, поломается ли на самом деле конструкция в любом заданном месте (цена ответа может составить, например, 64 тыс. долларов), зависит от того, может ли упругая энергия перейти в энергию разрушения так, чтобы образовать трещину.

* Теоретическое максимальное растягивающее напряжение, требуемое для того, чтобы действительно "оттянуть" атомы друг от друга, на самом деле весьма велико и много больше реальных значений прочности, определяемых посредством обычных испытаний материалов на растяжение.

Современную механику разрушения занимает прежде всего не вопрос о нагрузках и напряжениях, а вопрос о том, как, почему, где и когда упругая энергия может перейти в энергию разрушения. Конечно, в простых случаях, когда имеют дело с веревками и стержнями, действует классическая концепция критического разрушающего напряжения, однако для больших или сложных конструкций, таких, как мосты, пароходы или сосуды высокого давления, она, как мы уже видели, страдает опасным переупрощением. Оказывается, что независимо от того, подвергается ли конструкция удару или действию статической нагрузки, разрушение путем разрыва зависит главным образом от следующего:

• 1) от цены в единицах энергии, которую нужно заплатить, чтобы протолкнуть трещину; 
• 2) от количества упругой энергии, которым располагает конструкция, готовая заплатить указанную цену; 
• 3) от размеров и формы наиболее опасных отверстий, трещин или дефектов конструкции. 

Тот факт, что величины энергии, необходимые для того, чтобы разрушить материал в любом данном поперечном сечении, для различных твердых тел весьма различны, легко подтвердить, ударив молотком сначала по стеклянной, а потом по консервной банке. Количество энергии, требуемое для разрушения материала, отнесенное к поперечному сечению, определяет его вязкость разрушения, или "трещиностойкость", которую в настоящее время чаще называют энергией или работой разрушения. Упомянутое свойство совершенно отлично и независимо от прочности материала на разрыв, которая определяется как напряжение (а не как энергия), требуемое для разрушения твердого тела. От трещиностойкости, или работы разрушения материала, в значительной мере зависит реальная прочность конструкции, особенно если она велика по размерам. А поэтому нам следует немного поговорить о работе разрушения различных типов твердых тел.

Энергия, или работа, разрушения

Когда твердое тело разрушается при растяжении, должна возникнуть хотя бы одна трещина, распространение которой разделяет кусок материала на части. Это означает, что должны образоваться по крайней мере две новые поверхности, не существовавшие ранее, до разрушения тела. Чтобы таким путем произвести в материале разрыв и образовать эти новые поверхности, необходимо разорвать все химические связи, до того сцеплявшие между собой поверхности.

Количество энергии, требуемое для разрыва почти всех типов химических связей, хорошо известно (по крайней мере химикам), и оказывается, что для большинства твердых тел, с которыми мы имеем дело в технике, общие количества энергии, требуемые для разрыва всех связей по любой единичной плоскости в любом поперечном сечении *, весьма близки между собой и не сильно отличаются от величины 1 Дж/м².

* Во многих случаях это количество энергии есть то же самое, что и поверхностная энергия, тесно связанная с поверхностным натяжением как жидкостей, так и твердых тел, и часто обсуждаемая в материаловедении.

Если мы имеем дело с материалами, которые носят название хрупких - к ним относятся камень, кирпич, стекло и фаянс, - упомянутое количество энергии и есть почти вся та энергия, которую мы должны сообщить телу, чтобы произвести разрушения. В действительности 1 Дж/м² - это совсем малое количество энергии. Так, согласно самой простой оценке упругая энергия, которую можно запасти в 1 кг сухожилий, достаточна для того, чтобы "заплатить" за 2500 м² свежей поверхности битого стекла. (Такое действие эквивалентно визиту слона в посудную лавку.) Вот почему каменщик раскалывает кирпич точно пополам всего лишь легким ударом мастерка, а чтобы разбить тарелку или бокал, достаточно малейшей неловкости.

Хрупкие материалы по возможности не используются там, где они могут подвергнуться действию растяжений. Эти материалы являются хрупкими в первую очередь не потому, что имеют низкую прочность на разрыв,- это означало бы, что для их разрушения требуется небольшая сила, - а потому, что для их разрушения требуется только небольшая энергия.

Технические и биологические материалы, которые используются в условиях растяжения и в этом смысле являются относительно безопасными, для образования новой поверхности при разрушении требуют значительно большей энергии. Другими словами, работа разрушения для них значительно (несравненно!) больше, чем в случае хрупких твердых тел. Для практически вязкого трещиностойкого материала величина работы разрушения обычно лежит в пределах 10³-10⁶ Дж/м². Поэтому энергия, требуемая для разрушения сварочного железа или мягкой стали, может быть в миллион раз больше энергии, требуемой для разрушения в таком же поперечном сечении стекла или керамики, хотя величины статической прочности на разрыв этих материалов не сильно различаются. Поэтому таблица значений прочности на разрыв, подобная табл. 2, в случае если ее используют для выбора какого-то конкретного материала, может дезинформировать конструктора. По этой же причине классическая теория упругости, основанная главным образом на силах и напряжениях, которая старательно разрабатывалась в течение столетий - и еще более старательно преподавалась студентам, - сама по себе не может правильно предсказывать разрушение реальных материалов и конструкций.

Таблица 4. Приближенные величины работы разрушения и прочности
при растяжении некоторых распространенных материалов

Хотя в деталях механизм поглощения столь огромных количеств энергии в виде работы разрушения в вязких трещиностойких материалах часто является тонким и сложным, общий принцип его действия весьма прост. В хрупком твердом теле работа, производимая в процессе разрушения, на самом деле сводится к той работе, которая необходима, чтобы разорвать химические связи на возникающей в процессе разрушения новой поверхности или в ее непосредственной окрестности. Как мы уже видели, соответствующая энергия мала и составляет около 1 Дж/м² В трещиностойком материале, несмотря на то что прочность и энергия каждой индивидуальной связи остаются теми же, изменения структуры материала в процессе разрушения распространяются на гораздо большую глубину. Практически эти изменения вполне могут распространяться на глубину свыше сантиметра, то есть на глубину, измеряемую 50 млн. атомов под видимой поверхностью разрушения. Поэтому если в процессе нагружения разорвется только одна межатомная связь, то энергия, требуемая для образования новой поверхности, увеличится в миллионы раз, что, как мы видели, и имеет место в действительности. Молекулы, находящиеся вдали от поверхности разрушения, способны, таким образом, поглощать энергию и вносить свой вклад в сопротивление разрушению.

Высокие значения работы разрушения мягких металлов обязаны в первую очередь пластичности этих материалов. Это означает, что при их растяжении кривая деформирования отклоняется от закона Гука при совсем небольших напряжениях, после чего материал начинает деформироваться пластически, подобно пластилину (рис. 21). Если стержень или лист из такого металла разрушается в результате растяжения, то, перед тем как произойдет разрыв, материал вытягивается словно патока или жевательная резинка. На концах в месте разрыва образец принимает коническую форму и выглядит примерно так, как показано на рис. 22. Такую форму разрушения часто называют шейкообразованием.

Рис. 21. Кривая деформирования для пластичного металла (мягкая сталь). Заштрихованная область представляет работу разрушения металла.
 

Рис. 22. Работа разрушения пропорциональна объему пластичсски деформированного металла (заштрихованная область) и поэтому, грубо говоря, пропорциональна t². Работа разрушения тонкого листа может быть очень малой.

а - металлическая плита большой тощины,
б - тонкий металлическии лист.

Шейкообразование и другие подобные формы пластического разрушения возможны потому, что многие из бесчисленных слоев атомов в кристаллах металла способны скользить относительно друг друга. Дислокационный механизм этого скольжения не только обеспечивает взаимное проскальзывание слоев подобно картам в колоде, но и поглощает энергию, и весьма большую. Результатом всех этих сдвигов, скольжений и смещений в кристаллах является то, что металл обретает способность значительного формоизменения и поглощения упругой энергии.

Дислокационный механизм скольжения *, постулированный первоначально Дж. Тейлором в 1934 г., был предметом интенсивных научных исследований в течение последних 30 лет. Он оказался исключительно тонким и сложным. Процессы, происходящие в столь, казалось бы, простой вещи, как кусок металла, оказались не менее хитроумными, чем большинство процессов в живых биологических тканях. Забавно, что этот хитроумный механизм, вероятно, не конструировался с какой-то определенной целью. Природа сама не может, так сказать, извлекать из него пользу, поскольку в своих конструкциях она никогда не использует металлы, которые и в самородках-то встречаются весьма редко. Однако дислокации в металлах оказались чрезвычайно полезными для инженеров, можно сказать, что они были изобретены для их пользы, поскольку именно благодаря дислокациям металлы не только обладают трещиностойкостью, но и допускают ковку, обработку давлением и одновременно упрочение.

* См. "Почему мы не проваливаемся сквозь пол", гл. 3 и 9, где дается элементарное представление о дислокациях; более полно вопрос освещен в книге: Cottrell A. The Mechanical Properties of .Matter (Wiley, 1964 etc.).

А вот у искусственно созданных пластиков и волокнистых композитов способы поглощения упругой энергии при разрушении иные. Механизм их совершенно отличен от механизма поглощения металлов, но достаточно эффективен. У биологических материалов также, по-видимому, имеются весьма совершенные механизмы получения больших величин энергии разрушения, которые работают весьма изощренным образом. Способ, реализующийся, например, в древесине, исключительно эффективен, и работа разрушения дерева, взятая на единицу веса, больше, чем для большинства сортов стали *.

* Снова см. "Почему мы не проваливаемся сквозь пол", гл. 8. 89

Продолжим теперь обсуждение вопроса о том, как упругая энергия в эластичной конструкции умудряется перейти в работу разрушения. Если угодно, в чем же действительная причина разрушения?
 

Гриффитс, или как жить в мире трещин и концентрации напряжений

Пускай их сколько угодно с бортов по волнам валяет, все лучше, чем с этой трещиной на поверхности баллера отведать килевой качки. Р. Киплинг. "Хлеб, отпущенный по водам"

Как было сказано в начале этой главы, все реальные конструкции имеют трещины, царапины, отверстия и другие дефекты. Корабли, мосты, самолеты подвержены разнообразным случайным воздействиям, которые приводят к зазубринам и надрезам, и мы должны научиться сосуществовать с ними, обеспечивая наибольшую возможную безопасность, хотя, согласно Инглису, для многих из таких дефектов локальные напряжения могут заметно превосходить справочные данные о прочности материала. Объяснение того, почему и как можно, вообще говоря, жить в окружении конструкций, несущих столь высокие напряжения, без катастроф, было выдвинуто Гриффитсом (1893-1963) в статье, опубликованной в 1920 г., как раз через 25 лет после прекрасного рассказа Киплинга о трещине. Поскольку в 1920 г. Гриффитс был никому не известным молодым человеком, на эту статью никто не обратил внимания. Во всяком случае, энергетический (несиловой) подход Гриффитса ко всей проблеме разрушения в то время да и в течение многих последующих лет был не только новым, но и совершенно чуждым самому духу инженерного мышления. Даже сегодня очень многие инженеры на самом деле не понимают, в чем состоит суть теории Гриффитса.

Сказанное Гриффитсом состоит в следующем. Инглисова концентрация напряжений с энергетической точки зрения является просто механизмом (чем-то вроде застежки-молнии) для превращения упругой энергии в энергию разрушения, подобно тому как электромотор является механизмом для превращения электрической энергии в механическую работу, а консервный нож является механизмом для использования мышечной энергии. Ни один из этих механизмов не будет работать, если не подводить к нему бесперебойно нужного рода энергию. Чтобы раздвинуть атомы материала, недостаточно одной только концентрации напряжений, а необходим еще подвод упругой энергии. Если подвод упругой энергии прекращается, останавливается и процесс разрушения.

Рассмотрим теперь образец из упругого материала, который сначала растянули, а затем закрепили его концы таким образом, чтобы он не мог больше ни получать, ни отдавать механическую энергию. Таким образом создалась механическая система, содержащая определенное количество упругой энергии. Если в этом растянутом материале начнет распространяться трещина, то требуемая работа разрушения должна быть полностью "оплачена" по энергетическому счету. Если для простоты мы примем, что наш образец является пластинкой материала единичной толщины, то требуемая энергия должна составить WL, где W - работа разрушения (на единицу площади), a L - длина трещины. Заметим, что речь здесь идет об "энергетическом долге", о том, что по энергетическому счету должно быть занесено в дебет, хотя никакого кредита в действительности получено не было. Дебет линейно возрастает с ростом длины трещины L.

Эта энергия должна быть немедленно изыскана во внутренних ресурсах, и, поскольку мы имеем дело с замкнутой системой, она может быть получена только за счет уменьшения упругой энергии внутри системы. Другими словами, где-то внутри образца должно уменьшиться напряжение. Такая ситуация возможна, поскольку берега трещины под действием напряжения немного разойдутся, а это немедленно приведет к уменьшению напряжения вблизи ее поверхности (рис. 23). Грубо говоря, две треугольные области, затененные на рисунке, и отдадут упругую энергию. Можно ожидать, что эти области с ростом длины трещины L будут в основном сохранять свои пропорции и поэтому их площадь будет расти как квадрат длины трещины, то есть как L². Следовательно, количество высвобождающейся упругой энергии будет расти как L².

Рис. 23. а - недеформированный образец;
б - образец растянут, и его концы жестко закреплены; система не может ни получать, ни отдавать энергию;
в - в растянутый образец внесена трещина. Напряжение в затененных областях уменьшается, и они отдают упругую энергию, которая может теперь пойти на дальнейшее распространение трещины.

Таким образом, суть принципа Гриффитса определяется тем, что, в то время как энергетический долг растет линейно с длиной трещины L, энергетический кредит растет как квадрат длины трещины L². Следствия этого изображены на рис. 24. Линия ОА представляет энергию, требуемую для образования новой поверхности растущей трещины, и это - прямая линия. Линия OВ представляет энергию, освобождаемую в системе при достижении трещиной данной длины, и это - парабола. Общий баланс энергии, являющийся алгебраической суммой двух упомянутых энергий, представляется линией ОС.

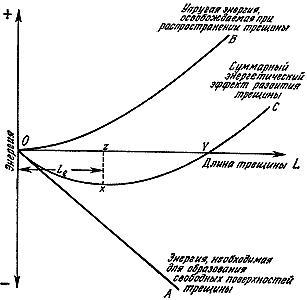
Рис. 24. Высвобождение энергии по Гриффитсу, или почему предметы разлетаются на куски.

До точки Х на графике система в целом должна поглощать энергию; после точки Х энергия начинает выделяться из системы. Отсюда следует, что существует некоторая критическая длина трещины, которую мы будем обозначать L_g и которая называется критической длиной трещины по Гриффитсу. Трещины, длина которых меньше L_g, не представляют опасности, они не могут расти сами по себе. Трещины же, имеющие длину больше L_g, растут "сами по себе" и поэтому весьма опасны*. Такие трещины чем дальше, тем быстрее распространяются по материалу и неизбежно ведут к "взрывному" (сопровождаемому шумом) разрушению. Конструкция заканчивает свое существование не с тихим всхлипом, а с грохотом и в большинстве случаев идет на свалку.

* Может показаться, что длина L_g должна соответствовать на графике отрезку OY, но по размышлении вы увидите, что это не так. Критической, или пороговой, по отношению к распространению трещины энергией, которую мы должны сообщить системе, является энергия, равная отрезку ZX. (Она и соответствует истинному "коэффициенту запаса".)

Наиболее важное следствие из всего сказанного состоит в том, что даже если локальное напряжение на концах трещин очень велико (даже если оно много больше, чем зарегистрированная в справочнике прочность материала), до тех пор пока в конструкции нет трещины или другого отверстия, длина которого превышает критическую длину L_g, конструкция безопасна и не разрушается. Именно это свойство позволяет нам не падать духом и не тревожиться слишком сильно по поводу инглисовой концентрации напряжений. Именно по этой причине отверстия, трещины и царапины представляют опасность ровно настолько, насколько они ее представляют на самом деле.

Вычислить величину L_g оказывается гораздо проще, чем можно было бы ожидать. Хотя математика, использованная Гриффитсом, не внушает особого доверия, результат вычислений обезоруживает своей простотой - можно сказать, что он блистательно прост. Оказывается, что

L_g = 1/p x (работа разрушения на единицу поверхности трещины / упругая энергия в единице объема материала)

а это можно выразить как

L_g = 2WE/ps²

где W - работа разрушения в Дж/м²,  Е - модуль Юнга в Н/м², s - среднее напряжение растяжения в материале вблизи трещины, не учитывающее концентраций напряжении, в Н/м²,  L_g - критическая длина трещины в м. *

* Упругая энергия, равная 1/2 es, может быть записана также как 1/2 s²L/E, поскольку Е = s/е.

Таким образом, предельная длина безопасной трещины зависит просто от величины отношения работы разрушения к упругой энергии, запасенной в материале. Эту длину можно рассматривать как обратно пропорциональную резильянсу. Вообще говоря, чем выше резильянс, тем меньше длина трещин, с которыми еще можно мириться. Это еще один пример двух качеств, одновременно не достижимых полностью.

Как мы видели выше, в резине можно запасти много упругой энергии. Однако работа разрушения для нее очень мала, а потому и критическая длина трещины L_g для растянутой резины тоже весьма невелика и обычно составляет доли миллиметра. Поэтому, когда мы протыкаем булавкой надутый воздушный шар, он взрывается с оглушительным шумом. Таким образом, хотя резина весьма эластична и ее можно сильно растянуть без разрушения, когда она все же разрушается, то происходит это "хрупким" образом, примерно так же, как у стекла.

Примером того, каким образом можно одновременно достичь и эластичности, и трещиностойкости, служат такие вещи, как одежда, плетеные корзины, деревянные корабли и конные экипажи. Все эти вещи содержат более или менее свободные и гибкие соединения, так что энергия расходуется на трение, о чем свидетельствуют их шуршание и скрип. Однако, хотя плетеные изгороди и птичьи гнезда очень хорошо противостоят внешним нагрузкам, принцип их создания почти не используется современными инженерами. (Одно из исключений составляют автомобильные покрышки, где в резину для борьбы с ее чрезмерной хрупкостью добавляется специальный корд.)

Из приведенной выше формулы видно, что длина L_g быстро уменьшается с ростом напряжения s. Поэтому, если мы хотим, чтобы при сравнительно высоких напряжениях оставались безопасными достаточно длинные трещины, следует использовать материалы, для которых велики работа разрушения W и жесткость, то есть модуль Юнга, Е. Именно этим объясняются столь широкое использование мягкой стали и ее значение не только в экономике, но и в политике; будучи весьма дешевой, она характеризуется как большой работой разрушения, так и высокой жесткостью.

Как мы увидим дальше, при использовании формулы Гриффитса возникает много подводных камней, поэтому мы не должны рассматривать ее как какое-то дарованное свыше решение всех проблем конструирования, но в то же время она проясняет некоторые проблемы конструирования, которым ранее не находили объяснения и которые были окружены предрассудками.

Например, вместо того чтобы, не утруждая себя, использовать совершенно фиктивные коэффициенты запаса прочности, сегодня мы можем попытаться спроектировать конструкцию, которая не будет разрушаться при наличии трещин заданной длины. Выбранная длина трещин будет зависеть от размеров конструкции, а также от возможных условий ее работы и контроля за ней. Если речь идет о возможных жертвах при разрушении конструкции, то вполне очевидна необходимость сделать так, чтобы безопасная трещина была настолько велика, дабы в пятницу после обеда ее и при плохом освещении разглядел скучающий и бестолковый контролер.

В действительно больших конструкциях, таких, как корабли или мосты, хотелось бы, чтобы и трещины длиной в 1-2 м не представляли опасности. Предположим, что мы ориентируемся на безопасную трещину длиной 1 м. Тогда даже при столь умеренном допущении, что работа разрушения стали составляет 10⁵ Дж/м², мы найдем, что такая трещина будет устойчивой вплоть до напряжений в 110 МН/м² (11 кгс/мм²). Но если мы захотим большей безопаности и будем ориентироваться на трещину длиной 2 м, допустимое напряжение придется уменьшить до 80 МНм² (8 кгс/мм²).

На самом деле 80 МН/м² - это как раз тот уровень напряжения, на который рассчитывают при проектировании крупных конструкций, и для мягкой стали это напряжение соответствует коэффициенту запаса прочности, лежащему между 5 и 6, и поэтому оно вполне приемлемо. Посмотрим, как все это работает на. практике. Из 4694 судов, проходивших в доке обычную проверку, у 1289, то есть более чем у четверти, были обнаружены серьезные трещины в корпусе, после чего, конечно, были предприняты необходимые меры по ремонту. Число же судов, которые, если бы не принятые меры, действительно разломились в море пополам, было все же много меньшим и составляло весьма малую долю от общего их количества. Одно такое судно пришлось примерно на каждые пятьсот кораблей. Если бы при конструировании этих судов были предусмотрены более высокие напряжения или их корпуса были изготовлены из более хрупкого материала, то в большинстве случаев трещины не были бы обнаружены до самого момента катастрофы.

Следуя доктрине Гриффитса в ее чистом виде, мы обнаружим, что трещины меньше критической длины вообще не могут распространяться, а поскольку любая трещина начинает свое существование с весьма малых размеров, то и вообще ничто никогда на разрушается. В действительности же, конечно, по многим веским причинам, которые составляют компетенцию металлургов и материаловедов, трещины до критической длины все же могут расти (см. гл. 14). Существенно, что, как правило, это происходит очень медленно, так что имеется достаточно времени для того, чтобы обнаружить эти трещины и что-то предпринять.

К несчастью, бывают и исключения. Профессор Дж.Ф.К. Конн, до недавнего времени занимавшийся в Глазго строительной механикой корабля, рассказал мне историю, как на крупном грузовом судне кок, прийдя как-то утром на камбуз готовить завтрак, обнаружил большую трещину посреди пола. Кок послал за старшим стюардом, который пришел, посмотрел на трещину и послал за старшим помощником капитана. Старший помощник пришел, посмотрел на трещину и послал за капитаном. Капитан пришел, посмотрел на трещину и сказал: "А, ничего страшного, дайте-ка мне позавтракать!"

Но у кока был явно научный склад ума и, разделавшись с завтраком, он достал краски, пометил концы трещины и поставил возле отметки дату. Через некоторое время корабль попал в непогоду и трещина удлинилась на несколько дюймов. Тогда кок нанес новую отметку и поставил новую дату. Он проделал это со всей добросовестностью еще несколько раз.

Когда судно в конце концов потерпело аварию, именно на той половине, которую удалось спасти и отбуксировать в порт, оказались отметки кока, которые, по мнению профессора Конна, служат самыми достоверными из всех свидетельств о процессе роста больших трещин докритической длины.

"Мягкая" сталь и "высокопрочная" сталь

Если конструкция не выдерживает нагрузок или имеются опасения относительно ее прочности, то естественное внутреннее чувство подсказывает инженеру, что надо использовать "более прочный" материал; если речь идет о стали, то это будет высокопрочная сталь. Для больших конструкций это, вообще говоря, ошибочное решение, поскольку ясно, что даже в случае мягкой стали ее прочность используется далеко не полностью. Это происходит потому, что, как мы уже видели, разрушение конструкции может определяться не прочностью, а хрупкостью материала.

Хотя измеряемые величины работы разрушения зависят от способа, которым производится соответствующее испытание, и здесь трудно получить однозначный результат, все же можно сказать, что трещиностойкость большинства металлов с ростом прочности несомненно уменьшается. На рис. 25 в качестве примера показано соотношение между этими двумя величинами в углеродистых сталях при комнатной температуре.

Рис. 25. Приближенное соотношение между прочностью и работой разрушения
для некоторых простых углеродистых сталей. (По В.Д. Бигсу)

Легко (и это не очень дорого) вдвое увеличить прочность мягкой стали путем повышения содержания углерода. Однако, если мы сделаем это, величина работы разрушения может уменьшиться раз в 15. В той же пропорции уменьшится и критическая длина трещины, то есть она при том же напряжении уменьшится от 1 м до 6 см. Если, однако, мы повысили вдвое и рабочее напряжение, то критическая длина трещины уменьшится в 15х2² = 60 раз. Таким образом, если критическая длина трещины первоначально была 1 м, теперь она составит 1,5 см, что было бы весьма опасно для большой конструкции.

Для конструктивных элементов малых размеров, таких, как болт или коленчатый вал, положение иное, здесь не имеет смысла ориентироваться на трещины метровой длины. Если мы хотим, чтобы допустимая предельная длина трещины равнялась, например, 1 см, то рабочее напряжение, при котором такая трещина остается безопасной, может достигать почти 280 МН/м² и в этом случае стоит применить высокопрочный материал. Таким образом, одно из следствий теории Гриффитса состоит в том, что в целом высокопрочные материалы и большие рабочие напряжения более безопасно применять в малых конструкциях, чем в больших. Чем больше конструкция, тем меньше напряжение, приемлемое с точки зрения безопасности. Это один из факторов, накладывающих ограничения на размеры судов и мостов.

Соотношение между работой разрушения и прочностью, подобное показанному на рис. 25, почти справедливо и для обычных углеродистых сталей. Можно добиться лучшего соотношения между прочностью и трещиностойкостью, если использовать легированные стали, то есть стали с присадками других элементов и уменьшенным содержанием углерода, но эти стали слишком дороги для применения в крупногабаритных конструкциях. В связи с этим около 98% всей выпускаемой стали - это "мягкая" сталь, другими словами, мягкий, или пластичный, металл с прочностью около 40-50 кгс/мм² (около 450 МН/м²).
 

О хрупкости костей

Вы - мальчишки, вы - девчонки, Ваши кости хрупки, тонки. Чтоб расти и ввысь стремиться. Вам не следует беситься. Р.Л. Стивенсон. "Детский цветник стихов"

Конечно, кости детей отнюдь не хрупки *, и Стивенсон писал очаровательный вздор. Кости развиваются из эмбрионального коллагена, или хрящевого вещества, прочного и вязкого, но не очень жесткого (его модуль Юнга около 600 МН/м²). По мере развития плода коллаген укрепляется тонкими неорганическими нитями, называемыми остеонами. Они образованы главным образом из извести и фосфора и имеют химическую формулу типа ЗСа₃(РО₄)₂ х Са(ОН)₂. В результате этого процесса армирования костей их модуль Юнга увеличивается примерно в 30 раз и достигает значения около 20000 МН/м². Однако проходит значительное время после рождения, прежде чем наши кости полностью насыщаются кальцием. Дети, естественно, более уязвимы в отношении механических травм, но в целом их кости, по-видимому, более эластичны и менее хрупки, чем кости взрослых, в чем можно убедиться на любом лыжном склоне.

* Очень редко, но возникают патологические состояния, при которых кости даже у совсем молодых людей делаются весьма хрупкими. Как сказал мне хирург-ортопед, причины этого заболевания медицина пока не постигла,

Однако все кости относительно хрупки по сравнению с мягкими тканями, а работа разрушения их, надо думать, меньше, чем работа разрушения дерева. Хрупкость костей ограничивает перегрузки, которым могут подвергать себя крупные животные. Как уже говорилось в связи с судами и машинами, гриффитсова критическая длина трещины является абсолютной, а не относительной величиной. Другими словами, она одна и та же и для мыши, и для слона, как одни и те же для всех животных прочность и жесткость костей.

Исходя из этого, можно заключить, что наибольший размер животного, который еще можно считать не представляющим особой опасности для его существования, лежит где-то вблизи размера человека или размера льва. Мышь, или кошка, или здоровый человек могут без вреда для себя спрыгнуть со стола, однако сомнительно, чтобы это мог сделать слон. И в самом деле, слоны должны быть очень осторожными; слон, который скачет или перепрыгивает через изгородь подобно овцам или собакам, - зрелище, весьма редкое. Особенно крупные животные, подобные китам, приспособлены к существованию только в море. Интересен пример с лощадьми. Дикие предки современной лошади были небольшими и, вероятно, не слишком часто ломали ноги. Но впоследствии человек вывел достаточно крупных лошадей, которые могли бы без устали работать на него, и эти несчастные создания постоянно ломают себе ноги.

Известно, что люди преклонного возраста особенно подвержены костным переломам, обычно это приписывается прогрессирующей с возрастом хрупкости костей. Последнее обстоятельство, несомненно, играет определенную роль, однако оно не всегда является определяющим фактором. Насколько мне известно, достоверных данных об изменении работы разрушения костей с возрастом не имеется, но, поскольку прочность костей за период между 25 и 75 годами уменьшается только примерно на 22%, не похоже, чтобы резко уменьшалась работа разрушения. Профессор Дж.П. Пол из университета Страйсклайда говорил мне, что результаты его исследований указывают как на более важную причину таких переломов на прогрессирующую потерю нервами контроля за натяжением мышц. Так, внезапный испуг может вызвать мышечное сокращение, достаточное для того, чтобы сломать, например, шейку бедра, даже если пациент не получил никакого удара извне. В таком случае человек, естественно, падает на землю (а, возможно, кроме того, и ударяется о какой-либо предмет), и в результате причиной перелома ошибочно считают падение, а не мышечный спазм. Говорят, что у некоторых африканских оленей подобные переломы задних ног случаются при виде льва.
 

Часть вторая. Конструкции, нагруженные растяжением

Оглавление

---

---

Март 2001