| В. Я. Френкель, Б. Е. Явелов
ЭЙНШТЕЙН:
Глава III Флуктуации и потенциал-мультипликатор |
| В. Я. Френкель, Б. Е. Явелов
ЭЙНШТЕЙН:
Глава III Флуктуации и потенциал-мультипликатор |
Где атомы - там флуктуации
Еще только приступившего к самостоятельным научным исследованиям Эйнштейна его близкий друг Бессо запомнил как "молодого человека со страстным интересом к науке, поглощенного проблемой осязаемости атомов и эфира" [1, с. 387]. В то время большинство физиков как бы махнули рукой на эти "вечные" вопросы и, смирившись с тем, что с их решением в лучшем случае придется подождать, занимались, как всем казалось, более важными и актуальными задачами. Эйнштейн же неуклонно продвигался в этом столь точно охарактеризованном Бессо направлении и в 1905 г. обоймой основополагающих работ поразил обе цели: в статье "О движении взвешенных в покоящейся жидкости частиц, требуемом молекулярно-кинетической теорией теплоты" [2] он дал экспериментаторам рецепт, как наблюдать атомные движения и измерять размеры атомов, а в статье "К электродинамике движущихся тел" [3] показал, что все попытки обнаружить эфир тщетны просто потому, что такового в природе не существует.
Но если эфир пал при первом же "выстреле", то для доказательства реальности атомов понадобилась тщательная "пристрелка". Вся серия первых работ Эйнштейна по молекулярной физике, начиная с написанной в 1900 г. статьи "Следствия из явлений капиллярности" [4], как это отмечал он сам в автобиографических заметках, была посвящена поиску "таких фактов, которые, возможно, надежнее устанавливали бы существование атомов конечной величины" [5, с. 148]. Последовательно приближаясь к этой цели, Эйнштейн уже в 1904 г. в статье "К общей молекулярной теории теплоты" [6] обращается к анализу флуктуационных явлений.
В одной популярной статье Эйнштейн так поясняет причину флуктуаций величины давления, действующего на стенку сосуда со стороны содержащегося в этом сосуде газа: "Отскакивающие от каждой единицы поверхности стенки молекулы газа оказывают на нее определенное среднее давление. Но действительно оказываемое моментальное давление не равно в точности среднему. Величина давления испытывает колебания, соответствующие хаотичному характеру молекулярных движений, обусловливающих давление" [7, с. 28].
В том, что, согласно кинетической теории материи, термодинамические величины должны флуктуировать, т.е. испытывать хаотические отклонения от средних, равновесных значений, отдавали себе отчет и классики статистической механики Л. Больцман и Дж. Гиббс (а еще ранее Р. Клаузиус, В. Томсон и Дж. Максвелл). Однако как тот, так и другой, отстаивая правомерность молекулярно-кинетической теории, стремились продемонстрировать полное согласие ее выводов с положениями термодинамики и доказывали, что флуктуации эти ввиду ничтожных размеров и огромного числа молекул слишком малы, чтобы оказывать какое-то ощутимое влияние на реально наблюдаемые процессы и явления.
Эйнштейн подошел к проблеме флуктуации с иной стороны, чем Больцман и Гиббс, он стал изыскивать как раз те экспериментальные ситуации, в которых эти флуктуации могли бы быть непосредственно наблюдены и измерены. На такой поиск его натолкнуло полученное в работе 1904 г. из самых общих исходных предположений фундаментальное выражение для среднего квадрата флуктуации энергии (e2) произвольной системы, состоящей из большого числа частиц:
e2 = kT2(dE/dT) (1)
(к - постоянная Больцмана, T - абсолютная температура, E. - средняя энергия системы). Из этого выражения видно, что константа Больцмана задает масштаб флуктуаций. Но ведь эта же постоянная определяет всю шкалу атомно-молекулярных величин соотношением k=R/N, в котором R - универсальная газовая постоянная - связана с числом Авогадро N (число частиц в грамм-молекуле, равное 6,02·1023). Величина 3/2 kT равна средней кинетической энергии одной молекулы при температуре Т.
У М. Планка есть интересное высказывание по поводу постоянной Больцмана:
“Эта константа принимает чрезвычайно малое значение, которое, естественно, стоит в тесной связи с энергией одной молекулы и точное значение которой приводит поэтому к вычислению массы молекулы и связанных с ней величин. Эта постоянная часто обозначается как больцмановская постоянная, хотя сам Больцман никогда не вводил ее. Насколько я знаю, это странное обстоятельство объясняется тем, что Больцман, как это, по-видимому, следует из его случайных высказываний, совершенно не думал о возможности точного измерения этой постоянной” [8, с. 607].Следует еще сказать, что Эйнштейн вывел соотношение (1), не зная, что оно (вместе со многими другими его результатами по статистической механике) двумя годами ранее уже получено Гиббсом [9], который, однако, не придал ему особого значения. Отметим также, что в этот же период к плодотворным исследованиям флуктуации приступил М. Смолуховский. Его первая статья по флуктуациям [10] была закончена им 3 июля 1903 г., а опубликована 24 апреля 1904 г. Статья Эйнштейна, о которой идет речь, датирована им 27 марта 1904 г.Итак, Эйнштейн начинает размышлять, как бы “увидеть” и измерить флуктуации; их наблюдение должно наконец непосредственно подтвердить реальность атомов, а измерения позволят точно определить и постоянную Больцмана, и число Авогадро, которые, по косвенным данным тех лет, были известны с точностью всего лишь 50% [11, с. 158]. Как результат таких поисков в 1905 г. появляется его знаменитая работа “О движении взвешенных в покоящейся жидкости частиц, требуемом молекулярно-кинетической теорией теплоты” [2], в которой было показано, что взвешенные в покоящейся жидкости мелкие, но все-таки вполне доступные наблюдению с помощью обычного микроскопа частицы в соответствии с молекулярно-кинетической теорией должны совершать беспорядочные микроскопические движения с беспрестанно меняющейся по величине и направлению скоростью. Причину этого движения легко понять: молекулы окружающей жидкости при своих хаотических тепловых колебаниях непрерывно и со всех сторон “бомбардируют” взвешенную частицу и, так как бомбардировка носит совершенно случайный характер, в каждый момент времени толчок, испытанный частицей в одном направлении, сильнее, чем в противоположном. Если частица крупная, размером, скажем, 1 мм, эти нескомпенсированные толчки ее с места не сдвинут. Если же частица достаточно мала, порядка 0,001 мм и меньше, она начинает “лихорадочно метаться” в жидкости.
Это явление беспрестанного хаотического блуждания взвешенных в жидкости микрочастиц получило название броуновского движения в честь английского ботаника Р. Броуна, впервые обнаружившего его в 1827 г. при наблюдениях под микроскопом взвеси цветочной пыльцы в воде. С тех пор было предложено множество объяснений броуновского движения, однако все они оставались словесными и их конкретная экспериментальная проверка не представлялась возможной. Кроме того, сами экспериментальные результаты были неотчетливы: фантастическое зрелище безостановочно мечущихся частиц гипнотизировало экспериментаторов, но какие характеристики явления нужно измерять, они не знали.
По поводу этой своей работы с объяснением старой загадки Эйнштейн впоследствии писал: “Не зная, что наблюдения над “броуновским движением” давно известны, я открыл, что атомистическая теория приводит к существованию доступного наблюдению движения микроскопических взвешенных частиц” [5, с. 149]. В самой статье, во вступительной части, говорится: “Возможно, что рассматриваемые движения тождественны с так называемым броуновским молекулярным движением, однако доступные мне данные относительно последнего столь неточны, что я не мог составить об этом определенного мнения” [2, с. 108]. Конечно, между этими высказываниями - а их, кстати сказать, разделяет более 40 лет - можно усмотреть некоторое противоречие, но, как бы там ни было, представляется несомненным, что в противоположность часто высказываемому мнению эта работа Эйнштейна появилась отнюдь не как попытка решить “загадку” броуновского движения *. Она была логическим результатом его планомерных поисков наблюдаемых флуктуационных явлений (флуктуационный характер броуновского движения ясен, ведь в среднем импульс, передаваемый взвешенным частицам молекулами жидкости, равен нулю).
* Аналогично тому как совершенно не соответствуют действительности часто встречающиеся суждения типа того, что теория относительности Эйнштейна возникла как интерпретация отрицательного результата опыта Майкельсона, а световые кванты были введены им для объяснения явлений фотоэффекта.Эйнштейн получает два важнейших результата - связь между коэффициентом диффузии броуновских частиц и постоянной Больцмана:D = kT/6phR (2)
(h - коэффициент вязкости жидкости, R - радиус частицы) и выражение для среднеквадратичного смещения частицы вдоль произвольного направления за время t:
(l2)1/2 = (2Dt)1/2 (3)
Этим результатам он придает решающее значение: их экспериментальное подтверждение докажет справедливость молекулярно-кинетической теории и позволит, наконец, точно определить фундаментальную постоянную Больцмана. Если же, наоборот, предсказания не оправдаются, то это будет “веским аргументом против молекулярно-кинетического представления о теплоте” [2, с. 108].
Решения важнейшего для физики вопроса о реальности атомов Эйнштейн ждет не от туманных натурфилософских рассуждений и не от бесконечных словопрений, а от прямого, так сказать “лобового”, опыта, причем, как видно, ждет с нетерпением. “Если бы какому-либо исследователю удалось вскоре ответить на поднятые здесь вопросы!” - таким восклицанием заканчивается статья. Для Эйнштейна эта статья не отвлеченная “игра ума”, не еще одна публикация в солидном журнале, укрепляющая его репутацию в научном мире; нет, ему чрезвычайно интересно, просто необходимо - и причем поскорее - убедиться в том, что атомы, о которых говорят уже более 2000 лет, действительно существуют. Как не похоже это на тщательно выверенный суховатый академический стиль, характерным образцом которого может служить следующее высказывание гениального Гиббса:
“... тот, кто основывает свою работу на гипотезах, касающихся строения материи, стоит на ненадежном фундаменте. Затруднения этого рода удержали автора от попыток объяснения тайн природы и заставили его удовлетвориться более скромной задачей вывода некоторых более очевидных положений, относящихся к статистической отрасли механики. При этом здесь уже не может быть ошибки с точки зрения согласия гипотез с фактами природы, ибо в этом отношении ничего не предполагается” [12, с. 14].В 1908 г. Ж. Перрен с сотрудниками серией тонких и систематических экспериментальных работ блестяще подтвердили все выводы Эйнштейна, касающиеся броуновского движения, и из прямых опытов получили для числа Авогадро значение, лежащее в пределах от 6,5·1023 до 7,2·1023 (современное значение 6,02·1023) и согласующееся с более ранними косвенными оценками [13]. После этих работ отрицать реальность атомов было уже невозможно. В том же году ярый противник атомизма В. Оствальд вынужден был признать:“Совпадение броуновского движения с требованиями кинетической гипотезы... дает теперь право самому осторожному ученому говорить об экспериментальном доказательстве атомистической теории материи. Таким образом, атомистическая теория возведена в ранг научной, прочно обоснованной теории” [14, с. IV].Но все это произошло, как уже говорилось, только в 1908 г., а пока Эйнштейн продолжает изыскивать возможные флуктуационный эксперименты. В декабре 1905 г. он заканчивает свою вторую статью по броуновскому движению [15], “дополняющую в некоторых пунктах” предыдущую работу. Новая статья носит название “К теории броуновского движения” (полученные Эйнштейном отклики на предыдущую публикацию убедили его в том, что “придуманный” им эффект действительно идентичен явлению, давно открытому английским ботаником).Один из “дополняющих пунктов” сводится к следующему. Если в первой работе для среднеквадратичного смещения броуновской частицы из формул (2) и (3) получалось выражение
(l2)1/2 = (t)1/2(kT/3phR)1/2 (4)
то теперь выводится значительно более общее соотношение:
(D2)1/2 = (t)1/2(2kTB)1/2 (5)
где (D2)1/2 - среднеквадратичное изменение за время t произвольного наблюдаемого параметра a системы, а В - “подвижность системы по отношению к параметру a ”.
Пусть на взвешенный в жидкости с коэффициентом вязкости h шар радиусом R в направлении оси Х действует сила F. По закону Стокса шар будет двигаться со скоростью v=F / (6phR). Если в данном случае за параметр a взять х - координату центра шара, то подвижностью в случае этого параметра будет отношение скорости, приобретаемой шаром под действием силы, к величине этой силы, т.е. B = 1/(6phR). Подставляя это значение в обобщенное соотношение (5), снова получаем (4).
Беря в качестве B отношение скорости вращения шара в жидкости к вызывающему это вращение вращательному моменту, Эйнштейн с помощью формулы (5) получает величину среднеквадратичного поворота шара за время t в результате “вращательного броуновского движения”.
Электрические флуктуации
Но соотношение (5) совершенно общее, и ниоткуда не следует, что сфера его применения ограничивается только механическим движением. И поэтому здесь впервые Эйнштейн обращает внимание на “электрические” флуктуации, которые также может описывать формула (5). В частности, он указывает, что по этой формуле можно рассчитать среднеквадратичное значение количества электричества, которое вследствие хаотического движения электронов проходит за время t через поперечное сечение проводника, замкнутого в кольцо. В этом случае в качестве подвижности следует взять отношение тока к электродвижущей силе, т.е. величину, обратную электросопротивлению кольца. Получающееся при этом выражение
(q2)1/2 = (t)1/2(2kT / r)1/2 (6)
(q - количество электричества, r - сопротивление) Эйнштейн не записывает и заканчивает этот параграф своей статьи несколько пессимистически: “Я не мог больше найти никаких следствий, доступных опытной проверке; поэтому исследование дальнейших возможностей мне кажется бесполезным” [15, с. 126 ].
Но через год в работе “О границе применимости теоремы о термодинамическом равновесии и о возможности нового определения элементарных квантов” [16] он снова возвращается к электрическим флуктуациям. В этой статье Эйнштейном был получен следующий замечательный по своей общности результат: для любой системы, в любых условиях средний квадрат флуктуации энергии, приходящийся на одну степень свободы, равен 0,5kT, т.е. средней энергии поступательного движения молекулы газа в одном направлении. Это положение можно трактовать как некоторое расширение классического закона равнораспределения, согласно которому в системе из большого числа частиц, находящейся при постоянной температуре T, энергия распределяется таким образом, что на каждую степень свободы в среднем приходится одинаковое количество энергии 0,5kT.
Полученный результат Эйнштейн сразу же использует для расчета флуктуационной разности потенциалов на электрическом конденсаторе. Конденсатор - система с одной степенью свободы, поскольку его энергия определяется значением единственной переменной - разностью потенциалов U между обкладками - по известной формуле E=0,5CU2, где С - электрическая емкость конденсатора. В согласии с новым выводом Эйнштейна и, следовательно, для среднеквадратичного значения флуктуационного напряжения на конденсаторе получается выражение
(U)1/2 = (kT / C)1/2 (7)
Таким образом, казалось бы, открывается путь “электрического” наблюдения флуктуации и определения константы Больцмана.
Эйнштейн рассчитывает величину ожидаемого флуктуационного напряжения при комнатной температуре для вполне доступного в изготовлении воздушного конденсатора из двух вдвинутых одна в другую систем металлических пластин по 30 штук в каждой; площадь пластины 100 см2, зазор между ближайшими пластинами двух наборов 1 мм. Получается весьма малая величина - 10-6 В. Но ее можно увеличить, выдвинув одну группу пластин из другой: заряд Q обкладок при этом не изменится, а напряжение возрастет согласно формуле U=Q/C, поскольку емкость сильно снизится.
Пусть при раздвижке пластин емкость конденсатора уменьшится в 500 раз, тогда подлежащее измерению напряжение достигнет 5·10-4 В. Раздвижка пластин конденсатора полезна и в другом отношении. Как измерить флуктуационное напряжение, если оно по самой своей природе беспрестанно и очень быстро изменяется не только по величине, но и по знаку? При быстром выдвигании одной группы пластин из другой “последнее” напряжение перед раздвижкой возрастет в C1/C2 раз (C1 - начальная, C2 - конечная емкость конденсатора) и станет равным (kT)(C1/C2)1/2, а “новое” флуктуационное напряжение на уже раздвинутом конденсаторе будет (kT/C2)1/2, т.е. в (C1/C2)1/2 раз меньше (для конкретного рассматриваемого конденсатора это отношение больше 20).
Как зарегистрировать электрические флуктуации
Итак, обладая достаточно чувствительным электрометром, можно попытаться зарегистрировать электрические флуктуации.
В то время физики уже располагали высокочувствительными электрометрами, в частности квадрантными, которые позволяли измерять напряжение порядка 10-6 В. Однако для эйнштейновской цели они не годились. В этих приборах энергия, требующаяся для отклонения их подвижной системы (у квадрантного электрометра это легкая металлическая пластинка - бисектор), черпается из цепи, в которой производят измерения (говоря современным языком, они нагружают измеряемую цепь). В то же время флуктуационное количество электричества на обкладках конденсатора при раздвижке остается столь же ничтожным, как и в исходном положении, а “замороженная” флуктуационная энергия, хотя и возрастает в C1/C2 раз (за счет работы против электростатических сил притяжения между разноименно заряженными пластинками), все равно остается очень малой: для рассматриваемого конденсатора при разрядке под напряжением 5·10-4 В и с током, скажем, 10-10 А ее хватит меньше чем на 5·10-4 с.
Но перспектива электрического измерения флуктуации весьма заманчива, и Эйнштейн задумывается, нельзя ли изобрести такой электрометр, который при измерениях в основном черпал бы энергию не из исследуемой цепи, а из какого-нибудь внешнего источника. Плод этих размышлений - небольшую заметку “Новый электростатический метод измерения малых количеств электричества” - он отсылает в печать в феврале 1908 г. [17]. Существо метода поясняет рис. 1, заимствованный из этой работы.
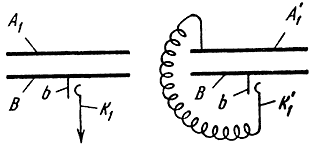
Рис. 1. Схема, поясняющая принцип действия потенциал-мультипликатора
Мимо двух металлических пластин A1, А'1 движутся жестко связанные (например, укрепленные на непроводящем вращающемся диске) металлические листочки B. Пусть на пластинку A1 подан малый электростатический потенциал, подлежащий измерению. Когда листочек В проходит под пластиной A1, его контактный штифт b касается неподвижной контактной пружины K1, соединенной с землей. При этом электрический заряд на пластине A1 индуцирует на листочке В равный по величине и противоположный по знаку заряд. Когда этот листок подходит под пластину A'1, он передает ей заряд, касаясь своим штифтом b пружины K'1. Если таких листочков много, то каждый, проходя под пластиной A1*, будет увеличивать ее заряд до тех пор, пока не наступит состояние, определяемое равновесием процессов накопления и утечки заряда. Если придать пластинам A1, А'1 форму скобы, охватывающей листочки с обеих сторон, стационарный потенциал пластины А'1 будет во много раз превышать исходный потенциал пластины А1.
Это можно объяснить следующим образом. В момент контакта штифта b с пружиной К' пластина А'1 приобретает потенциал (относительно земли), равный потенциалу листочка и определяемый соотношением P=Q/C (Q - заряд листочка, С - его емкость относительно земли). В то же время емкость листочка В в этом положении тем меньше, чем в большей степени пластина А'1 его охватывает, “перерезая исходящие из его зарядов силовые линии электрического поля” (По этому же принципу работают известные электростатические генераторы Ван де Граафа, развивающие электрические потенциалы в миллионы вольт).
Пусть теперь n одинаковых элементов типа, показанного на рис. 1, включены последовательно. Если коэффициент усиления, или, как тогда говорили, коэффициент мультипликации, одного элемента равен а, то конечный стационарный потенциал многокаскадной схемы будет an. Из этого следует, что уже при скромных значениях a и n можно получить очень большое усиление, а значит, и весьма высокую чувствительность при измерениях малых количеств электричества и низких электрических потенциалов.
Важнейшее достоинство предлагаемого Эйнштейном прибора состоит в том, что требующаяся для измерения энергия (например, энергия, необходимая для поворота стрелки электроскопа, измеряющего потенциал пластины А'1 оконечного каскада) черпается не из той цепи, где производятся измерения, а из внешнего источника, - это работа, затрачиваемая механическим приводом, перемещающим листочки против сил электростатического притяжения и отталкивания.
От идеи к измерительному прибору
Короткая заметка Эйнштейна заканчивается призывом: “...Я надеюсь, что кто-нибудь из физиков заинтересуется этим предложением. Я охотно сообщу ему свои дальнейшие соображения по этому вопросу” [17, с. 154]. Заметка датирована 13 февраля 1908 г., однако из эйнштейновского письма А. Зоммерфельду, написанного месяцем ранее, видно, что еще до публикации идеи измерительного метода его автор уже составил себе представление о конкретных путях ее практической реализации.
В декабре 1907 г. в Мюнхенском университете, где кафедру экспериментальной физики возглавлял уже всемирно известный В.К. Рентген, а теоретической - ставший знаменитым несколько позже А. Зоммерфельд, место приват-доцента получил ученик Рентгена П. Кох, только что защитивший докторскую диссертацию, посвященную прецизионным измерениям теплоемкости. Планы дальнейшей экспериментальной деятельности Коха определились не сразу, и в связи с этим Эйнштейн предложил Зоммерфельду для новоиспеченного приват-доцента работу, “к выполнению которой у меня очень лежит сердце”. Далее в письме пояснялось: “Речь идет об измерительной электростатической машинке, с помощью которой можно будет сделать доступными для измерений гораздо меньшие количества, чем это позволяют современные электрометры” [18].
Заинтересовать мюнхенцев все же не удалось, и бернский патентный эксперт решил действовать самостоятельно. 30 июля в письме своему первому, еще, как сказали бы сейчас, “неформальному” ассистенту Я. Лаубу Эйнштейн сообщает: “Я нашел здесь (в Берне - Авт.) искусного механика, который сейчас по моим указаниям изготовляет для меня электростатическую машинку. В ближайшие дни она будет готова. Я хочу сам убедиться, что она может работать и что россказни насчет коварства контактов справедливы” [19]. Из этого отрывка видно, что, во-первых, Лаубу уже известно об эйнштейновском замысле и что, во-вторых, сведущие в электротехнике сразу же указали на подвижные контакты как на самое “узкое” место предложенного устройства. Похоже, что эта трудность впоследствии оказалась фатальной для судьбы изобретения. Вскоре Лауб был извещен о первых достижениях:
“Машинка готова и хорошо работает в случае больших напряжений. Для того чтобы экспериментировать с напряжениями менее 0,1 В, я соорудил электрометр и источник напряжения. Вам не отделаться усмешкой, когда Вы увидите тот шедевр, что я сварганил. Но в Берне нет никакого электрометра, а я хочу, наконец, внести в вопрос ясность. Во всяком случае, те результаты, которые пока получены, обнадеживают” [19].Эйнштейн почему-то умалчивает о том, что к этому времени он уже изыскал возможность работать, хотя бы урывками, над электростатической машинкой в профессиональной лаборатории. Ему удалось заинтересовать своим замыслом А. Гоккеля (1860-1927), профессора космической физики (принятый в то время термин означал тогда совсем не то, что в нашу эпоху) университета во Фрейбурге, что в часе с небольшим езды на поезде от Берна. Гоккель, который наряду с метеорологией и оптикой атмосферы занимался также атмосферным электричеством и радиоактивностью, видимо, был не прочь заполучить в свои руки сверхчувствительный электрометр и гостеприимно распахнул двери подведомственного ему физического кабинета перед бернским энтузиастом, наведывавшимся во Фрейбург обычно по воскресеньям.Сохранилось несколько документов, касающихся сотрудничества Эйнштейна с Гоккелем [19]. Так, выясняется, что он приезжал к Гоккелю 16 мая 1908 г., а 28 июня проработал в его лаборатории с девяти утра до пяти вечера. В открытке Гоккелю со штемпелем “Берн. 3.12.1908” говорится:
“Я заказал себе здесь у одного хорошего механика вторую машинку и сам построил весьма чувствительный электрометр. Так что теперь у меня есть то, что я могу назвать своего рода собственной «лабораторией». К настоящему моменту я определил, что с помощью машинки можно измерять напряжения до 10-4 В - чувствительность недостижимая, когда количества измеряют без вспомогательного заряда. Если метод окажется пригодным для измерения в сто раз меньших напряжений, ничто больше не помешает прямому экспериментальному доказательству существования границ справедливости электростатики, определяемых молекулярной теорией”14 декабря Эйнштейн писал И. Штарку о “маленькой лаборатории для электростатических исследований, которую соорудил из примитивных средств для разработки одного электростатического метода” [20].Значительно больше подробностей сугубо технического свойства содержится в эйнштейновском письме Гоккелю от 9 марта 1909 г.:
“Глубокоуважаемый господин профессор.Небезынтересно, что возникшая у Эйнштейна еще в 1907 г. мысль поручить разработку электростатической машинки какому-нибудь молодому физику долго не оставляла его. В 1909 или 1910 г. такая попытка - и снова неудачная - была предпринята в отношении чистого теоретика Лауба, Эйнштейн познакомился с директором Физического института Фрейбургского университета Йозефом Ковальским (1866-1927) - польским физиком, исследователем люминесценции, впоследствии занимавшим посты польского посла в Ватикане, Голландии и Турции. Прощупывалась возможность предоставления Лаубу места ассистента Ковальского с тем, чтобы Лауб вместе с Гоккелем работал над эйнштейновским изобретением. Впрочем, может быть, Эйнштейну хотелось устроить Лауба (с которым он уже к тому времени написал две статьи по теории относительности) поближе к Берну, чтобы облегчить совместную работу.В соответствии с Вашим дружеским приглашением я прибуду в Фрейбург в воскресенье (9 апреля - Авт.) в пять часов, если до того не получу от Вас никаких вестей. Я совершенно согласен с тем, чтобы нам с Вами заняться испытаниями с имеющимися ртутными контактами. Если у Вас есть немного времени для подготовки (экспериментов - Авт.), то я попросил бы Вас о следующем:
1) подогнать эбонитовую шайбу так, чтобы все проволочки могли погружаться в ртутные капли;Последнее особенно важно, поскольку в таком случае мы можем надеяться установить для данного варианта достижимые пределы погрешностей (определяемые контактами).2) приготовить бензин для протирания эбонитовых деталей;
3) приготовить электрометр, с помощью которого мы сможем измерять напряжение 10-3 В.
С наилучшими пожеланиями, преданный Вам А. Эйнштейн”.
В последний раз Эйнштейн и Гоккель встретились 7 марта 1913 г. в Цюрихе, где в то время проходил ежегодный съезд швейцарского Общества естествоиспытателей. Гоккель был приглашен к Эйнштейну на ужин, на котором присутствовали еще несколько видных швейцарских физиков, а также братья Конрад и Пауль Габихт. Имеются все основания полагать, что младший Габихт, Пауль, как раз и был тем “искусным механиком”, о котором Эйнштейн писал Лаубу и Гоккелю.
Как уже говорилось в предыдущей главе, К. Габихт, с которым Эйнштейн познакомился еще в Поли и которого он в 1905 г. агитировал поступить в бернское патентное бюро [21, с. 73], завершал свое математическое образование в местном университете. В Берне Эйнштейн, Соловин и К. Габихт часто собирались вместе для бесед на философские и литературные темы. Свой кружок они в шутку именовали “Академия Олимпия”. Биограф великого физика К. Зелиг сообщает: “Частым гостем супругов Эйнштейн стал и младший брат Конрада, Пауль. На ординарных заседаниях «Академии», проходивших чаще всего на квартире Эйнштейна, Пауль варил кофе по-турецки и беседовал с Эйнштейном о приборе для измерений малых напряжений, который они вместе мастерили” [21, с. 57].
Пауль Габихт в те времена, видимо, не слишком увлекался “высокими материями”, его гораздо больше интересовала техника. Со временем он стал автором целого ряда изобретений. Любопытно, что им было получено по меньшей мере четыре патента на усовершенствование кофеварки. Как знать, может быть, эти конструкции рождались в его голове, когда он готовил кофе для философствовавших “действительных членов Академии”!
Братья Габихт неизменно фигурируют во всех эйнштейновских жизнеописаниях - но только в связи со своим великим другом. О них самих, как правило, почти ничего не сообщается. Поэтому резонно, может быть, дать о них краткое представление.
Конрад Габихт (1876-1958) родился в Шафхаузене, изучал математику в университетах Цюриха, Мюнхена, Берлина и Берна, где в 1903 г. защитил докторскую диссертацию. В дальнейшем всю жизнь преподавал математику и физику в школах Швейцарии, увлекался греческой философией, великолепно играл на скрипке [22].
Пауль Габихт (1884-1948), также родом из Шафхаузена, учился там ремеслу точной механики на фирме “Amsler und Co”, посещал техникум в Винтертуре, в 1910-1912 гг. работал в одной приборостроительной фирме в Базеле. Помимо упоминавшихся уже кофеварок и потенциал-мультипликатора, изобретал также другие прецизионные электроизмерительные приборы, коротковолновые приемники и устройства для УВЧ-терапии. Заядлый музыкант-любитель, П. Габихт увлекался усовершенствованием динамиков, а также механических электромагнитных граммофонных звукоснимателей, работал над ультразвуковыми устройствами. Время от времени он организовывал небольшие фирмы по мелкосерийному производству того или иного разработанного им оборудования. В области теории П. Габихт много размышлял над проблемами размерности физических величин и опубликовал статьи: “Структура физического закона” и “Знание и познание” [23].
С подключением к работам П. Габихта дела с “машинками” пошли веселее. Из письма Эйнштейна М. Бессо от 17 ноября 1909 г. видно, что замысел оправдывается: “Был там (в Цюрихе - Авт.), и Габихт с машинками. 1/10000 часть вольта достижима” [24, с. 14]. Наверное, где-то в это же время мультипликатором стал заниматься и старший Габихт.
В мае 1910г. братья Габихт посылают в “Physikalische Zeitschrift” небольшую заметку “Электростатический потенциал-мультипликатор по А. Эйнштейну” [25], в которой они описывают конструктивную реализацию эйнштейновской идеи и сообщают данные испытаний.
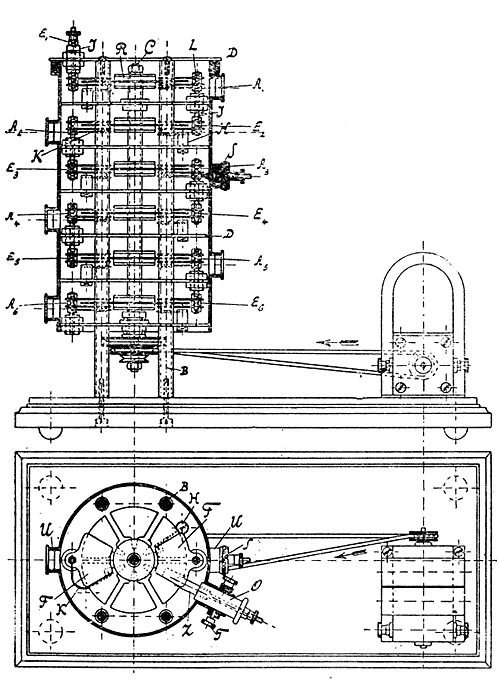
Рис 2. Схема потенциал-мультипликатора Эйнтейна-Габихта
Устройство прибора показано на рис. 2. Электродвигатель вращает вал С, на котором через изоляторы R укреплены металлические секторообразные листочки F. Эти листочки при вращении вала поочередно касаются контактных пружин Н и К таким образом, что разрыв обоих контактов происходит в момент, когда каждый из листочков F находится между парами входных Е и выходных А пластин. Прибор состоит из шести включенных последовательно ступеней. Подлежащий измерению малый потенциал подается на входную клемму Е1, а усиленный снимается с выходной клеммы А6. Видно, что устройство совершенно аналогично предложенному Эйнштейном. Прибор снабжен еще клеммами Е2-Е6 и А1-А5 для измерения коэффициентов усиления последовательных ступеней и дополнительным устройством О для компенсации паразитных разностей потенциалов.
Испытания прибора, в которых, как сообщают авторы, принимал участие Эйнштейн, проводились в лаборатории Цюрихского университета. Было показано, что коэффициент усиления (мультипликации) потенциала составляет 360000, а чувствительность прибора, ограниченная “плаванием нуля”, т.е. нестабильность нулевого показания прибора в условиях отсутствия потенциала на его входе, около 3·10-4 В; кроме того, была продемонстрирована линейность рабочей характеристики прибора, а также независимость коэффициента усиления от колебаний скорости вращения вала (при номинальной скорости вращения 1500 об./мин).
Габихты перечисляют следующие преимущества нового устройства по сравнению с популярным в то время квадрантным электрометром: низкая входная емкость (что позволяет измерять малые количества электричества), отсутствие высоковольтной батареи, независимость результатов измерений от температурных колебаний и механических сотрясений, возможность использования в качестве демонстрационного прибора (выходная клемма может быть соединена с обычным электроскопом); отмечается также, что потенциал-мультипликатор может оказаться весьма полезным в исследованиях радиоактивности. В заключение авторы выражают благодарность профессору Эйнштейну за неоценимое содействие и помощь в работе.
Но работа над потенциал-мультипликатором па этой публикации не заканчивается. В октябре 1911 г. Эйнштейн пишет Бессо из Праги:
“Габихт значительно усовершенствовал свою машинку. Колебания (очевидно, речь идет о том, что физики называют “плаванием нуля” - Авт.) стали почти в десять раз меньше. Откуда они происходят - еще не ясно и сейчас. Если внести еле заметные следы изоляционной массы на подвижный листочек первого каскада, то получается огромный разброс и колебания сильно возрастают. Поверхности, движущиеся друг относительно друга, должны быть металлическими. <...> Габихт опробовал стали на стали. Получилось, однако, очень плохо, и наблюдается значительный износ материала. При использовании системы сталь-латунь конец стальной пружины покрывается слоем латуни” [25, с. 27-28].В конце 1911 г. состоялась публичная демонстрация прибора перед немецкими физиками и электротехниками. Об этом говорится в эйнштейновском письме к Бессо от 26 декабря: “Габихт демонстрировал свою машинку в Берлинском физическом обществе и имел колоссальный успех. Им намного превзойден струнный электрометр” [24, с. 33 ]. В письме к Бессо от 4 февраля Эйнштейн не может удержаться, чтобы снова не вспомнить о впечатлении, произведенном мультипликатором. “Об успехе, который он (П. Габихт - Авт.) имел в Берлине, я уже тебе, конечно, сообщал. Там чуть ли не прыгали от восторга” [24, с. 36].Новый прибор незамедлительно попадает в энциклопедический курс физики петербургского профессора О.Д. Хвольсона. В главе об электрических измерениях (написанной А.Л. Гершуном) говорится:
“Особенно интересен мультипликатор, построенный Габихтом по идее Эйнштейна, в этом приборе потенциал повышается последовательно шестью ступенями, причем n (коэффициент мультипликации - Авт.) между первой и последней ступенью равен 360000. Благодаря столь огромному коэффициенту мультипликации при помощи этого прибора могут быть замечены и измерены на обыкновенном калиброванном электроскопе потенциалы порядка десятитысячных долей вольта” [26, с. 132].Дальнейшая судьба потенциал-мультипликатора Таким образом, перед потенциал-мультипликатором открывались, казалось бы, самые блестящие перспективы. В уже цитировавшемся письме к Бессо, в котором говорится о демонстрации прибора в Берлине, Эйнштейн с энтузиазмом сообщает своему другу: “...его (Габихта. - Авт.) будущее обеспечено. Меня это очень радует. У Габихта уже довольно много заказов” [24, с. 33 ].
Мы располагаем лишь одним свидетельством о попытке практического использования прибора Эйнштейна-Габихтов. Известный немецкий физик В. Герлах (соавтор замечательного опыта Штерна-Герлаха) вспоминает, что весной 1913 г. в Цюрихе Эйнштейн предложил ему, тогда начинающему физику, провести с помощью электростатической “машинки” измерения контактных разностей потенциалов между различными металлами. Дело в том, что в своем объяснении фотоэффекта Эйнштейн, кроме представления о выбивании электронов квантами света, ввел представление о работе выхода, неодинаковой у разных металлов (при контакте двух металлов эта разность работ выхода должна проявляться как контактная разность потенциалов). Планк критиковал эйнштейновское рассмотрение фотоэффекта не только за введение квантов, но и за использование второй - произвольной, как он считал, гипотезы о работе выхода. Научному руководителю Герлаха, известному физику Ф. Пашену, идея работы понравилась, и он, как пишет Герлах, приобрел у “базельского механика” (т.е., очевидно, у П. Габихта) новый измерительный прибор. Исследования начались, но, несмотря на все старания, определенных результатов получено не было. Но “виноват” был не потенциал-мультипликатор: Герлах указывает, что важнейшее упущение состояло в недостаточном контроле чистоты поверхностей изучавшихся металлов [27].
Р. Фюрт, известный в прошлом специалист по статистической физике, вспоминал, что, когда он в 1912 г. стал студентом Немецкого университета в Праге, он не застал там Эйнштейна, переехавшего из Праги в Цюрих в августе 1912 г. “Но повсюду - продолжал Фюрт, - были его (Эйнштейна - Авт.) следы. Так, например, в шкафу (физического кабинета - Авт.) хранилась машинка для мультипликации электрических зарядов” [28, с. 20]. Доктор Б. Глаус, заведующий научно-историческими коллекциями библиотеки цюрихского политехникума, любезно переслал нам неопубликованную справку об эйнштейновском потенциал-мультипликаторе, составленную Е. Вэккерлином, бывшим сотрудником бернского патентного бюро.
Вэккерлин сообщает, что его поиски сохранившихся экземпляров прибора в Берне и Винтертуре (в 26 км от Цюриха), где в те давние времена работал П. Габихт, не увенчались успехом. В то же время Вэккерлин приводит выдержку из хранящегося в архиве бернского патентного бюро и не опубликованного полностью доклада, с которым И. Заутер выступил в 1955 г. по радио Лозанны. Бывший сослуживец Эйнштейна указал, что в бернском почтово-телеграфном ведомстве (напомним, что в начале века оно находилось в одном здании с патентным бюро) “имеется модель аппарата, изобретенного Эйнштейном и позволяющего измерять очень малые напряжения; чувствительность аппарата пропорциональна скорости вращения ведущего вала”. Вэккерлин полагает, что речь идет об одном из ранних вариантов прибора, в котором для приведения во вращательное движение использовался не электродвигатель, а ручной привод наподобие применявшегося, например, в швейных машинках.
То, что некоторое количество потенциал-мультипликаторов все же было изготовлено, подтверждает и демонстрация в 1979 г. на выставке в Берлине, посвященной 100-летнему юбилею Эйнштейна, электростатической машинки под серийным номером 18.
Однако, насколько можно об этом судить из литературы того времени, последний раз мультипликатор упоминается в хвольсоновском “Курсе физики” 1914 г. (в более поздних изданиях этого курса он не упоминается). О подававшем столь радужные надежды приборе уже никто не вспоминает (даже сами его разработчики).
В чем тут дело? Имеются две главные причины. Во-первых, прибор все-таки, что называется, “не пошел”. Как это видно из ряда писем Эйнштейна к Бессо, конструкторы с самого начала постоянно мучились с контактами к вращающимся листочкам, - эти контакты изнашивались, загрязнялись, служили источниками паразитных сигналов [24, с. 14, 27-28]. В последнем из эйнштейновских писем к Бессо, в котором еще говорится о мультипликаторе, сообщается об использовании золоченых контактов (естественное с современной точки зрения решение) - именно это и принесло успех берлинской демонстрации прибора. Однако удовлетворительным образом справиться с проблемой контактов, видимо, не удалось. Впрочем, для современного физика совершенно очевидно, что прибор для измерения малых напряжений не должен содержать трущиеся контакты.
Вторая же причина угасания интереса к потенциал-мультипликатору состоит в том, что в это время уже начинала свое триумфальное шествие электронная лампа (усилительный вакуумный триод был запатентован американцем Ли де Форестом в 1907 г.), конкурировать с которой в слаботочных схемах контактной электростатической машинке было не под силу.
Достигнутая Габихтами чувствительность 3·10-4 В была все же недостаточна для выполнения поставленной Эйнштейном задачи измерения флуктуационного напряжения порядка 5·10-4 В (для сколько-нибудь приемлемой точности измерений чувствительность должна быть на порядок выше). Но и сама эта задача уже утратила былую актуальность, поскольку к концу первого десятилетия нашего века Ж. Перрену и ряду других исследователей удалось разными способами осуществить достаточно точные измерения константы Больцмана и числа Авогадро.
В своей заметке братья Габихт сообщали, что приступают к производству мультипликаторов в собственной мастерской и что ими подана соответствующая патентная заявка [25, с. 535]. К. Зелиг уточняет, что “патентная заявка и описание совместно разработанного прибора” были составлены Эйнштейном [21, с. 57]. Но был ли получен патент? Беседуя в 1930 г. с Р. Тагором, Эйнштейн припомнил, что не запатентовал свой “аппарат для измерения очень маленьких напряжений” [29]. Значит, изобретение не было запатентовано. Это кажется несколько странным. Действительно, П. Габихт был, видимо, довольно практичным человеком с предпринимательской жилкой, а что касается Эйнштейна, то уж лучшего помощника по патентованию вряд ли можно было желать. Кроме того, как об этом будет говориться в дальнейшем, в последующие годы Эйнштейн и сам получал патенты и не раз, “тряхнув стариной”, оказывал помощь как патентный эксперт.
Может быть, дело в том, что при ближайшем рассмотрении идея и даже конструкция прибора оказались в общем-то не столь уж новыми. Не в духе Эйнштейна было перед решением какой-либо задачи изучать сначала всю имеющуюся по данному вопросу литературу: создавая теорию относительности, он не имел ясного представления об опыте Майкельсона; разрабатывая теорию флуктуации, он “открыл” для себя уже давно известное броуновское движение. Не произошло ли нечто подобное и с потенциал-мультипликатором? По существу, этот прибор есть не что иное, как одна из разновидностей электростатической машины влияния *. Кстати, в период активной работы над потенциал-мультипликатором ни Эйнштейн, ни его друзья не употребляют этого широко используемого в электростатике термина - “электростатическая машина влияния”. С другой стороны, в написанном уже в 1952 г. письме к Бессо Эйнштейн вспоминает, что П. Габихт конструировал для него машину влияния [1, с. 465 ]. Может быть, этот термин вошел в его лексикон из формулировок возражений патентного ведомства относительно новизны его изобретения.
* Электростатическими машинами влияния в электростатике называют машины, в основу которых положен принцип наведения заряженным телом (через влияние, т.е. без гальванического контакта) заряда в первоначально нейтральном проводнике. От электростатических машин трения машины влияния отличаются, в частности, тем, что они в противоположность последним для своего возбуждения нуждаются в подведенном извне заряде.Электростатические машины (в том числе машины влияния) начали изобретать еще в конце XVIII в. По мере совершенствования этих приборов стало возможно использовать их в качестве источников заряда или, вернее, электроэнергии. Одним из первых решил такую задачу в 1865 г. профессор Рижского политехнического института А. Тёплер. Его статья называлась “О получении сильных электрических токов особого рода с помощью электрометра влияния” [30].Машина Тёплера, задача которой, таким образом, прямо противоположна задаче эйнштейновского мультипликатора, конструктивно довольно близка к последнему, что естественно, поскольку используется тот же основной принцип электростатического влияния и накопления заряда.
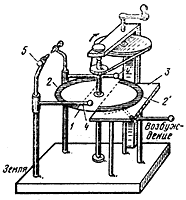
Рис. 3. Электростатическая машина Тёплера
Принцип действия машины Тёплера поясняет рис. 3. На выполненном из изоляционного материала диске 1 закреплена пара не соединяющихся между собой металлических полуколец 2, 2'. При вращении диска полукольца проходят над неподвижным индуктором 3 в виде плоской металлической пластины, на которую подан малый исходный потенциал возбуждения. Щетки 4, 4' соединяют каждое из полуколец с землей в момент, когда их емкость по отношению к индуктору 3 максимальна, и с выходным электродом 5, когда эта емкость минимальна, а, следовательно, потенциал максимален. В результате этого потенциал выходного электрода по отношению к земле непрерывно возрастает, пока не будет достигнуто динамическое равновесие с утечкой заряда.
К началу нашего столетия об электростатических машинах в общем-то забыли почти всюду, кроме учебных физических кабинетов. Их вытеснили электромагнитные машины с проволочными обмотками. Этим может и объясняться недостаточная осведомленность Эйнштейна и его друзей в области электростатических машин.
Интерес к электростатическим машинам вновь пробудился только к началу 30-х годов, когда американский физик Р. Ван де Грааф высказал идею, а затем и построил свой знаменитый высоковольтный генератор с полым шаровым электродом, развивавший потенциал до 1,5·106 В [31]. Как известно, в этом генераторе заряд непрерывно переносится бесконечной транспортерной лентой внутрь шарового электрода и по законам электростатики распределяется на его внешней поверхности, потенциал которой постоянно растет. Вдохновленный успехами генераторов Ван де Граафа академик А.Ф. Иоффе выдвигает в конце 30-х годов идею о возможности замены традиционных электромагнитных генераторов промышленной электроэнергетики электростатическими [32 ]. Под его руководством в Ленинградском физико-техническом институте развернулись работы по созданию мощных электростатических генераторов (с началом войны они были прерваны). Основной задачей этих работ было повышение КПД и мощности, приходящейся на единицу объема (или веса) генератора. И тут снова пришлось перейти от транспортерной ленты Ван де Граафа к компактным многодисковым конструкциям типа Тендера и Эйнштейна-Габихтов.
После войны разработки мощных электростатических генераторов дискового типа были возобновлены и у нас в стране, и за рубежом. Хотя идея перехода от электромагнитной электроэнергетики к электростатической не оправдалась, ряд моделей мощных и компактных электростатических генераторов с успехом используются в различных отраслях народного хозяйства.
Небезынтересно отметить еще одно обстоятельство. Сам Ван де Грааф в основополагающей статье о генераторе, получившем впоследствии его имя, в качестве своего непосредственного предшественника указывает В. Томсона (лорда Кельвина), который еще в прошлом веке предложил два типа потенциал-мультипликаторов. В одном из этих мультипликаторов перенос заряда осуществлялся транспортерной лентой, а в другом - водяными каплями [31].
В 1924 г. Эйнштейн должен был написать в журнал “Naturwissenschaften” заметку к 100-летию со дня рождения В. Томсона. Стояла нелегкая задача: дать на двух-трех страницах представление о научных достижениях “одного из наиболее сильных и плодотворных мыслителей XIX столетия” [33]. “Чем пытаться охватить все работы Томсона, я лучше покажу четкость работы его исследовательской мысли на нескольких примерах, которые меня в свое время особенно восхитили" - пишет в своей короткой заметке Эйнштейн. В качестве первого из трех таких примеров он выбирает томсоновскую установку для получения высоких напряжений с помощью водяных капель, т.е. именно то устройство, на которое потом сослался и Ван де Грааф.
Последующее развитие учения об электрических флуктуациях
Какова же дальнейшая судьба впервые рассмотренных Эйнштейном электрических флуктуации, для измерения которых и был задуман потенциал-мультипликатор? Их исследование было непосредственно продолжено Гертрудой де Гааз-Лоренц [34], дочерью великого голландского теоретика Г. Лоренца и женой известного физика-экспериментатора В. де Гааза, которая за свой неизменный интерес к проблемам этого рода получила в кругу друзей шутливое прозвище “броуновское движение” [35, с. 147]. Эта исследовательница детально рассмотрела флуктуационные явления в различных электрических цепях и электромеханических системах.
Эйнштейн взялся за разработку чувствительного прибора с целью обнаружения флуктуации, исторический же путь развития оказался обратным: экспериментаторы непосредственно столкнулись с флуктуациями в период освоения слаботочной техники, когда были созданы электроизмерительные приборы с чувствительностью 10-8 - 10-10 А по току и 10-5 - 10-6 В по напряжению, а также усилители на электронных лампах, обладающие огромными коэффициентами усиления по напряжению, току и мощности. Выяснилось, что дальнейшее повышение чувствительности наталкивается на принципиальные трудности, связанные с электрическими флуктуациями [36].
В первое время после изобретения электронной лампы казалось, что простым увеличением числа ламп в усилителе можно достичь неограниченно высоких коэффициентов усиления, а это позволит регистрировать сколь угодно слабые сигналы. Практика показала, однако, что это не так: улавливанию слабых сигналов всегда препятствовали “шумы”, которые были непосредственно слышны, когда к выходу усилителя подключали телефоны. Сначала думали, что эти шумы возникают из-за разного рода случайных механических и электромагнитных воздействий на усилитель, из-за нестабильности электропитания, наличия остаточных газов в вакуумных лампах и т.д.
В 1918 г. немецкий физик, ученик M. Планка, В. Шоттки первым понял [37], что даже при полном устранении всех этих возможных источников шумов некоторый шумовой фон в усилителе все-таки должен остаться. Его причина - статистический характер испускания электронов катодом лампы: поток “дробинок” - электронов, бомбардирующих анод, флуктуирует во времени (это явление Шоттки назвал дробовым эффектом), значит, ток, идущий через лампу, испытывает хаотические колебания, а это равносильно подсоединению на ее вход источника хаотического шумового сигнала *.
* Любопытно, что Шоттки впервые заинтересовался флуктуациями, прослушав в Берлине лекцию Эйнштейна по статистической механике [38].В начале 30-х годов правильность представлений Шоттки о дробовом эффекте была подтверждена экспериментально, причем из измерений этого эффекта удалось даже получить величину электрического заряда электрона, находящуюся в хорошем согласии со значениями, полученными другими методами [35, с. 59-71].И разработчики и потребители высокочувствительных гальванометров все более четко осознавали, что подвижная часть прибора (рамка, магнитная стрелка) никогда не прекращает каких-то беспорядочных микроколебаний около равновесного положения. Сначала все “сваливали” на сотрясения лабораторных помещений, микросейсмические толчки и старались освободиться от них, используя разного рода массивные, плавающие и амортизированные платформы. Таким образом, спустя сто лет повторилась примерно та же ситуация, что возникла после открытия Броуна, когда ученые всячески пытались остановить движение взвешенных в жидкости частиц, устраняя влияние сотрясений, тепла и света. Однако со временем стало ясно, что эти дрожания - чрезвычайно досадные, поскольку они ограничивают порог чувствительности приборов никакими техническими ухищрениями устранить невозможно. На то, что эта трудность принципиальная, связанная с броуновским движением подвижной части приборов, впервые указал шведский физик Г. Изинг в 1919 г. К началу 30-х годов это было надежно подтверждено, причем из данных по флуктуационным движениям рамки высокочувствительного гальванометра удалось с хорошей точностью определить константу Больцмана [36, с. 191].
В 1927 г. Дж. Джонсон с помощью высококачественного лампового усилителя непосредственно измерил тепловые шумы (и их температурную зависимость), возникающие за счет флуктуационного движения электрических зарядов в проводниках (углеродистые нити, металлические пленки, растворы электролитов), подключенных к входу усилителя, и, определив константу Больцмана, решил именно ту задачу, которую Эйнштейн поставил еще в 1905 г.
С начала 30-х годов учение об электрических флуктуациях усилиями многих физиков и радиоинженеров постепенно приобретает статус самостоятельного и необходимого для практических приложений раздела радиотехники и радиофизики. Уместно отметить, что важную роль в развитии теории электрических флуктуаций сыграли работы советских ученых - Ю.А. Круткова, Б.И. Давыдова, М.А. Леонтовича, С.М. Рытова.
За Эйнштейном прочно закрепился эпитет “творец теории относительности”. Широкий публике меньше известно, что и в развитии квантовой теории его заслуги едва ли не решающие. То, что Эйнштейн вместе со Смолуховским явился основоположником теории флуктуации известно еще меньше. И наконец, почти совсем забыт тот факт, что Эйнштейн первым обратился к изучению электрических флуктуации, т.е. тех самых шумов которые так “усложняют жизнь” радиотехникам, радиофизикам, радиоастрономам, а зачастую и радиослушателям При этом, имея в виду тему нашей книги, в заключение этой главы еще раз подчеркнем тот факт, что электрическими флуктуациями Эйнштейн занимался не только и не столько как теоретик, но и как экспериментатор и изобретатель.
Литература
1. Einstein A. - Besso M. Correspondance, 1903-1955. P.: Hermann, 1972.
2. Эйнштейн А. О движении взвешенных в покоящейся жидкости частиц, требуемом молекулярно-кинетической теорией теплоты // Собр. науч. тр. М.: Наука, 1966. Т. 3. С. 108-117.
3. Эйнштейн А. К электродинамике движущихся тел // Там же. 1965. Т. 1. С. 7-35.
4. Эйнштейн А. Следствия из явлений капиллярности // Там же 1966. Т. 3. С. 7-17.
5. Эйнштейн А. Творческая автобиография // Эйнштейн А. Физика и реальность. М.: Наука, 1965. С. 131-166.
6.Эйнштейн А. К общей молекулярной теории теплоты // Собр науч. тр. М.: Наука, 1966. Т. 3. С. 67-74.
7. Эйнштейн А. Теоретическая атомистика // Эйнштейн А. Физика в реальность. М.: Наука, 1965. С. 20-33.
8. Планк М. Возникновение и постепенное развитие теории квантов // Избр. тр. М.: Наука 1975. С. 603-612.
9. Эйнштейн А. Замечания к работам П. Герца "О механических основах термодинамики" // Собр. науч. тр. М.: Наука, 1966. Т. 3. С. 28.
10. Smoluchowski M. Unregelmassigkeiten in der Verteilung vop Gasmolekeln und deren Einlus auf Entropie und Zustandg-Gleichung // Boltzmann - Festschrift. Leipzig, 1904. S. 626-633.
11. Эйнштейн А. Элементарная теория броуновского движения // Собр. науч. тр. М.: Наука, 1966. Т. 3. С. 155-163.
12. Гиббс Дж. Основные принципы статистической механики. М.; Л.: Гостехтеоретиздат, 1946.
13. Перрен Ж. Атомы. М.: Госиздат, 1923.
14. Ostwald W. Grundriss der Allgemeinen Chemie. Leipzig: Teubner, 1909.
15. Эйнштейн А. К теории броуновского движения // Собр. науч. тр. М.: Наука, 1966. Т. 3. С. 118-127.
16. Эйнштейн А. О грапице применимости теоремы о термодинамическом равновесии и о возможности нового определения элементарных квантов // Там же. С. 145-151.
17. Эйнштейн А. Новый электростатический метод измерения малых количеств электричества // Там же. С. 152-154.
18. Eckert M., Pricha W. Die ersten Briefe Albert Einstein an Arnold Sommerfeld // Phys. Bl. 1984. Bd. 40. S. 29-34.
19. Laub J. J. Albert Einstein und Albert Gockel // Academia Friburgensis. 1962. Bd. 20. S. 30-33.
20. Hermann A. Albert Einstein und Johannes Stark: Brief wechsel und Verhaitnis der beiden Nobelpreistrager // Sudhoffs Arch. 1966. Bd. 50. S. 267-285.
21. Зелиг К. Альберт Эйнштейн. М.: Атомиздат, 1966.
22. Habicht M. Conrad Habicht // Verb. Schweiz. Naturforsch. Ges. 1959. Bd. 47. S. 405-406.
23. Russenberg M. F. Paul Habicht als Ingenieur und Wissenschafter // Mitt. Naturforsch. Ges. Schaffhausen. 1949. Bd. 23. S. 302-308.
24. Переписка А. Эйштейна и М. Бессо, 1903-1955 // Эйнштейновский сборник, 1974. М.: Наука, 1976. С. 5-112.
25. Gabicht С. und P. ElektrostatischerPotentialmultiplikator nach A. Emstem // Phys. Ztschr. 1910. Bd. II. S. 532-535.
26. Хвольсон О. Д. Курс физики. СПб., 1914. Т. 4.
27. Gerlach W. Erinnerung an Albert Einstein // Phys. Bl. 1979. Bd. 35. S. 93-102.
28. Fuhrt R. Personal reminiscences // Einstein: The first hundred years. L.: Methuen, 1980. P. 19-25.
29. Tagor talks with Einstein // Asia. 1931. Mar. 31. P. 138-142.
30. Toepler A. Ober die Erzeugung eines eigenthumlichen Art vor intensiven elektrischen Stromen vermittelst eines Influenz-Elektrometers // Ann. Phys. 1865. Bd. 5. S. 469-473.
31. Van de Graaf B. J. et al. The electrostatic production of high voltage for nuclear investigations // Phys. Rev. 1933. Vol. 43. P. 149-167.
32. Иоффе А. Ф. Электростатический генератор // ЖТФ. 1939. Т. 9, вып. 29. С. 2071-2090.
33. Эйнштейн А. К столетию со дня рождения лорда Кельвина (26 июля 1824 г.) // Эйнштейн А. Физика и реальность. М.: Наука, 1965. С. 97-99.
34. Haas-Lorentz G. L. de. Die Brownsche Bewegung und einige verwandte Erscheinungen. Braunschweig: Vieweg, 1913.
35. Эренфест - Иоффе. Научная переписка. Л.: Наука, 1973.
36. Грановский В. Л. Электрические флуктуации. М.; Л.: Изд-во Наркомата тяжелой пром-сти СССР, 1936.
37. Schottky W. Spontane Stromschwankungen in verschieden Elekrizitat-Leitern // Ann. Phys. 1918. Bd. 57. S. 541-560.
38. Welker H. W. Schottky // Solid State Electron. 1976. Vol. 19. P. 817-818.